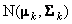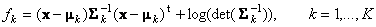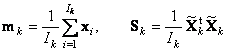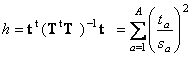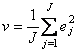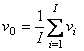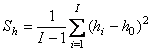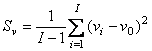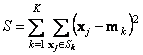Классификация
Содержание
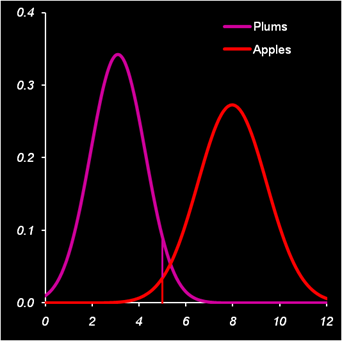
ВведениеВ этом документе рассмотрены наиболее популярные методы классификации, применяемые в хемометрике. Текст ориентирован, прежде всего, на специалистов в области анализа экспериментальных данных: химиков, физиков, биологов, и т.д. Он может служить пособием для исследователей, начинающих изучение этого вопроса. Продолжить исследования можно с помощью указанной литературы. В пособии интенсивно используются понятия и методы, описанные в других материалах по хемометрике: статистика, матрицы и векторы, метод главных компонент. Читателям, которые плохо знакомы с этим аппаратом, рекомендуется изучить, или, хотя бы просмотреть, эти материалы. Кроме того, здесь интенсивно используется специальная надстройка (Add-In) к программе Excel, которая называется Chemometrics.xla. Подробности об этой программе можно прочитать в пособии Проекционные методы в системе Excel. Изложение иллюстрируется примерами, выполненными в рабочей книге Excel Irix.xls, которая сопровождает этот документ. Предполагается, что читатель имеет базовые навыки работы в среде Excel, умеет проводить простейшие матричные вычисления с использованием функций листа, таких как МУМНОЖ, ТЕНДЕНЦИЯ и т.п. В отличие от других пособий из серии, здесь не удается один раз провести проекционные вычисления, а затем использовать их в разных методах. Поэтому некоторые листы книги Iris.xls не будут работать без использования Chemometrics Add-In. Важная информация о работе с файлом Iris.xls Ссылки на примеры помещены в текст как объекты Excel. 1. Базовые сведения1.1. Постановка задачиКлассификацией называется процедура, в которой объекты распределяются по группам (классам) в соответствии с численными значениями их переменных, характеризующими свойства этих объектов. Исходными данными для классификации является матрица X, в которой каждая строка представляет один объект, а каждый столбец – одну из переменных. Эта матрица называется исходным набором данных. Число объектов (строк в матрице X) мы будем обозначать буквой I, а число переменных (строк в матрице X) – буквой J. Число классов мы будем обозначать буквой K. Классификацией называют не только саму процедуру распределения, но и ее результат. Употребляется также термин распознавание образов (pattern recognition) , который можно считать синонимом. В математической статистике классификацию часто называют дискриминацией. Метод (алгоритм), которым проводят классификацию, называют классификатором. Классификатор переводит вектор признаков объекта x в целое число, 1, 2, … , соответствующее номеру класса, в который он помещает этот объект. 1.2. Обучение: с учителем и безЕсли для всех объектов исходного набора известно, к какому классу они принадлежат, то такая постановка задачи называется классификацией с учителем (или с обучением). Обучение без учителя происходит тогда, когда принадлежность объектов в исходном наборе нам заранее не известна. 1.3. Типы классовКлассификация может делаться для разного числа классов. Классификация с одним классом проводится в том случае, когда нам нужно установить принадлежность объектов к единственной выделенной группе. Например, отделить яблоки от всех остальных фруктов в корзине. Двухклассная классификация – это наиболее простой, базовый случай, который чаще всего называют дискриминацией. Например, разделить яблоки и груши, при условии, что никаких других фруктов в корзине нет. Многоклассовая классификация часто сводится к последовательности: либо одноклассных (SIMCA), либо двухклассных (LDA) задач и является наиболее сложным случаем. В большинстве случаев классы изолированы и не пересекаются. Тогда каждый объект принадлежит только к одному классу. Однако могут быть задачи и с пересекающимися классами, когда объект может относиться одновременно к нескольким классам. 1.4. Проверка гипотезВ математической статистике рассматривается задача проверки гипотез, которая, по сути, очень близка к классификации. Поясним это на простом примере. Пусть имеется смесь слив и яблок, которую надо автоматически разделить. Очевидно, что в среднем сливы меньше яблок, поэтому задачу можно легко решить, используя подходящее сито. Анализ размеров объектов показал, что они хорошо описываются нормальными распределениями со следующими параметрами. Сливы: среднее 3, дисперсия 1.4. Яблоки: среднее 8, дисперсия 2.1. Таким образом, разумно будет выбрать сито диаметром 5. .
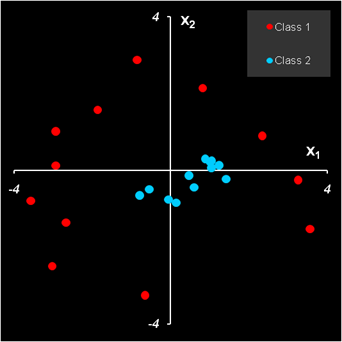
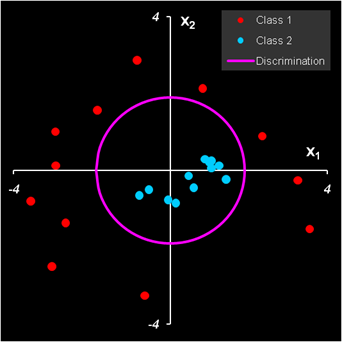
Рис. 1 Распределение объектов по размерам С точки зрения математической статистики в этой задаче мы проверяем гипотезу о том, что среднее нормального распределения равно 3 (слива), против альтернативы 8 (яблоко). Проверка происходит по одному единственному наблюдению x. Критическое значение равно 5: если x<5 (область принятия гипотезы), то гипотеза принимается (объект – слива), если x>5, то принимается альтернатива (объект – яблоко). 1.5. Ошибки при классификацииОчевидно, что в рассмотренном выше примере классификация не является идеальной – мелкие яблоки попадут в класс слив, а крупные сливы останутся вместе с яблоками. Используя распределения объектов по размерам, можно рассчитать вероятности этих событий. α=1–Φ(5| 3, 1.4)=0.05 β=Φ(5| 8, 2.1)=0.01 где Φ– это кумулятивная функция нормального распределения. Для расчетов в Excel можно использовать встроенную функцию NORMDIST (НОРМРАСП). Величина α (ложное отклонение ) называется ошибкой первого рода, а величина β (ложное принятие) – ошибкой второго рода. Если поменять местами гипотезу и альтернативу, то ошибка 1-го рода станет ошибкой 2-го рода, и наоборот. Таким образом, при этом критическом уровне, 5% слив будет потеряно, и 1% яблок примешается к сливам. Если уменьшить критическое значение до 4, то примеси яблок практически не будет, зато потери слив достигнут 20%. Если же его увеличить до 6, то потери слив уменьшатся до 1%, но примесь яблок будет уже 5%. Понятно, что в этой задаче невозможно выбрать такое сито, которое правильно разделяло бы сливы и яблоки – всегда будут ошибки. При проверке гипотезы (классификации) важно понимать, какую ошибку важнее минимизировать. Приведем два классических примера. В юриспруденции, при гипотезе "невиновен", руководствуясь презумпцией невиновности, необходимо минимизировать ошибку 1-го рода – вероятность ложного обвинения. В медицине, при гипотезе "здоров", необходимо минимизировать ошибку 2-го рода – вероятность не распознать болезнь. Можно ли одновременно уменьшить обе ошибки? Да, в принципе, можно. Для этого надо изменить саму процедуру принятия решения, сделав ее более эффективной. Одним из главных способов является увеличение числа переменных, характеризующих классифицируемые объекты. В нашем примере такой новой, полезной переменной мог быть цвет – синий для слив, и зеленый для яблок. Поэтому в хемометрике применяют методы классификации, основанные на многомерных данных. 1.6. Одноклассовая классификацияДля случая одного класса ошибка первого рода α называется уровнем значимости. Ошибка 2-го рода для такой классификации равна 1 – α. Объяснение этому парадоксальному факту очень простое – альтернативой одному классу является все оставшееся мыслимые объекты, лежащие вне этого класса. Поэтому, какой бы классификатор мы не использовали, всегда найдется объект, не лежащий в этом классе, но очень похожий на объекты из него. Допустим, для примера, что мы отбираем сливы, отличая их от всего прочего, существующего на свете. Тогда, тщательно изучив придуманный нами метод классификации, можно создать искусственный объект (например, пластмассовый муляж), который подходит по всем выбранным критериям. 1.7. Обучение и проверкаКлассификатор (помимо вектора переменных x) зависит от свободных (неизвестных) параметров. Их надо подобрать так, чтобы минимизировать ошибку классификации. Подбор параметров называется обучением классификатора. Эта процедура проводится на обучающем наборе Xc. Помимо обучения, необходима еще и проверка (валидация) классификатора. Для этого должен использоваться новый проверочный набор данных Xt. Альтернативой валидации с помощью проверочного набора является проверка с помощью метода кросс-валидации. Между классификаций и калибровкой есть много общего. С теоретической точки зрения классификацию можно рассматривать как регрессию, откликом которой являются целые числа 1, 2, …, – номера классов. Напрямую этот подход используется при классификации методом PLS-дискриминации, который рассмотрен ниже. Также как и в калибровке, в классификации имеется большая опасность переоценки, которая в задачах классификации называется переобучением. Для того чтобы избежать этой опасности, надо внимательно следить за тем, как, при усложнении классификационного алгоритма, меняются ошибки в обучении и в проверке. 1.8. Проклятие размерностиВ задачах классификации имеет место проблема, которая поэтически называется проклятием размерности (Curse of dimensionality). Суть дела в том, что при увеличении числа переменных J сложность задачи возрастает экспоненциально. Поэтому, даже относительно скромное их число (J>10) может доставить неприятности. Заметим, что в хемометрических приложениях (например, при анализе спектральных данных) может быть и 1000 и 10000 переменных. В классических методах классификации большая размерность приводит к мультиколлинеарности, которая проявляется как вырожденность матрицы XtX, которую надо обращать в методах линейного и квадратичного дискриминационного анализа. В методах, опирающихся на расстояния между объектами (например, kNN), большая размерность приводит к усреднению всех расстояний. Основным способом решения этой проблемы являются методы понижения размерности, прежде всего метод главных компонент 1.9. Подготовка данныхПри решении задач классификации исходные данные должны быть соответствующим образом подготовлены, аналогично тому, как это делается в методе главных компонент. Например, центрирование данных автоматически заложено в алгоритм многих методов классификации. Особую роль в классификации играет преобразование данных. Поясним это на примере. На Рис. 2 показаны данные, принадлежащие двум классам. На левом рисунке они представлены в "натуральном" виде, а на правом рисунке – те же данные, но в полярных координатах
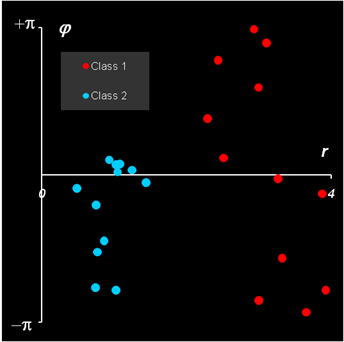
Рис. 2 Объекты в декартовых и полярных координатах Ясно, что в исходных декартовых координатах разделить классы очень сложно. Зато в полярных координатах дискриминация очевидна. .
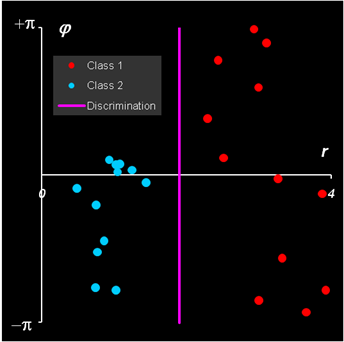
Рис. 3 Классификации в полярных координатах и ее образ в декартовых На Рис. 3 показана такая классификация и ее образ в исходных, декартовых координатах. На этом простом принципе основаны нелинейные методы классификации, например, метод опорных векторов 2. Модельные данные2.1. ПримерДля иллюстрации различных методов классификации мы будем использовать знаменитый пример – Ирисы Фишера, помещенный в рабочую книгу Iris.xls. Этот набор данных стал популярным после основополагающей работы, в которой Роберт Фишер предложил метод линейного дискриминационного анализа (LDA). Набор данных включает три класса по 50 образцов в каждом. Каждый класс соответствует виду ириса: Iris Setosa (класс 1), Iris Versicolour (класс 2) и Iris Virginica (класс 3). .
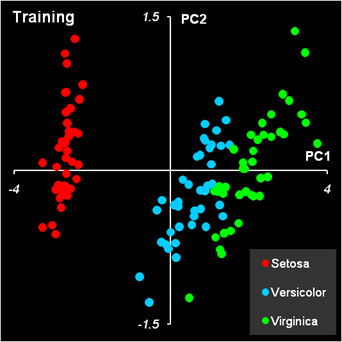
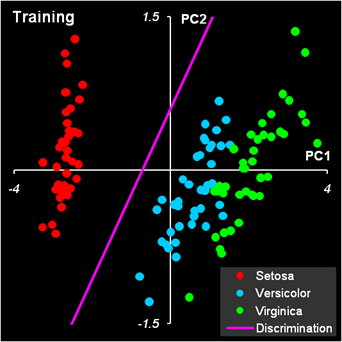
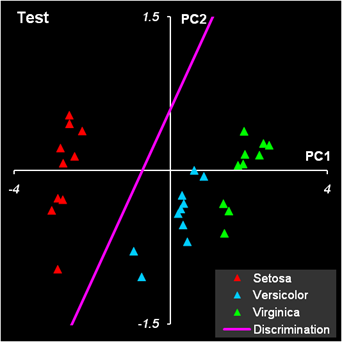
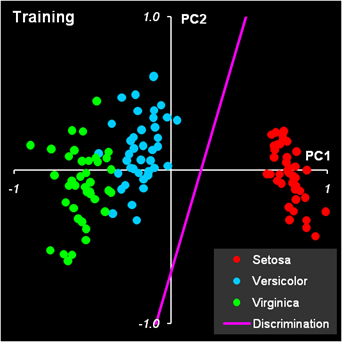
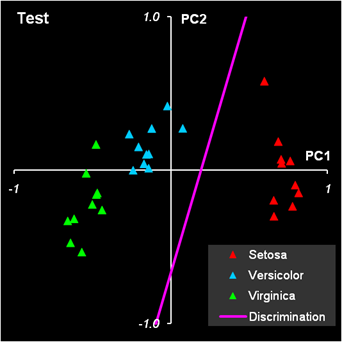
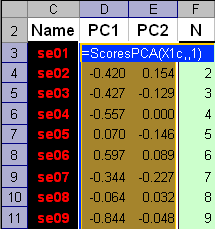
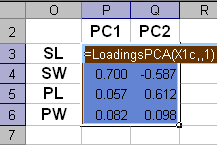
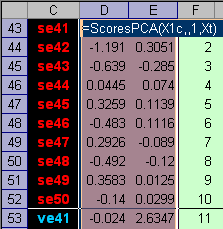
Рис. 4 Ирисы Фишера (слева направо): Setosa, Versicolour и Virginica В своей работе Р. Фишер использовал данные, собранные американским ботаником Э. Андерсоном, который измерил следующие характеристики цветков каждого из 150 образцов:
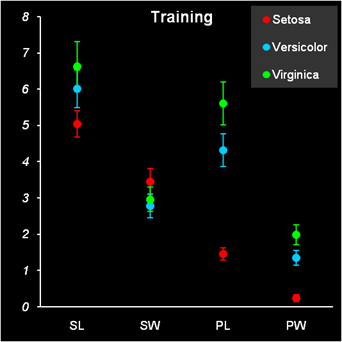
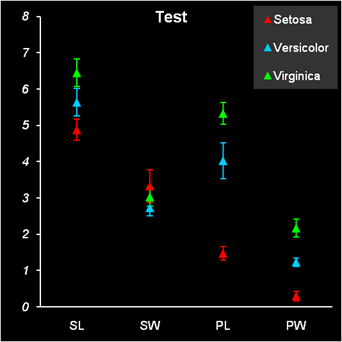
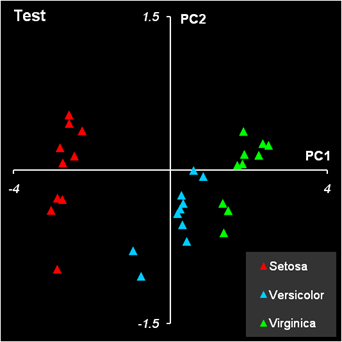
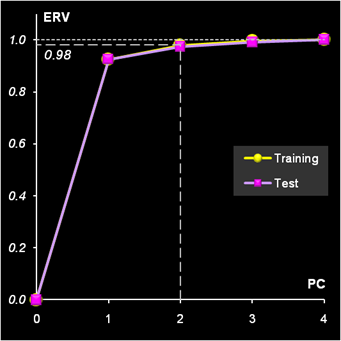
Все эти значения (в см) приведены в таблице на листе Data. Пытаясь понять, где у ирисов чашелистики, а где лепестки, естественно заглянуть в Wikipedia . Там сказано следующее. "Соцветия ириса имеют форму веера и содержат один или более симметричных шестидольных цветков. Растут они на коротком стебельке. Три чашелистика направлены вниз. Они расширяются из узкого основания в обширное окончание, украшенное прожилками, линиями или точками. Три лепестка, которые иногда могут быть редуцированными, находятся в вертикальной позиции и частично скрыты основанием чашелистика. У более мелких ирисов вверх направлены все шесть доль. Чашелистики и лепестки отличаются друг от друга. Они объединены у основания в цветочный цилиндр, который лежит над завязью" Однако, в русскоязычной Википедии (да и на многих других сайтах) утверждается следующее. "Цветки ирисов очень своеобразны: у них нет чашелистиков и лепестков." Оставим ботаников разбираться в этой проблеме. 2.2. ДанныеИсходный массив данных (3 класса по 50 образцов) был разбит на две части: обучающую и проверочную. В первое подмножество Xc вошли по 40 первых образцов из каждого класса (всего 120 образцов), а во второе подмножество Xt – оставшиеся в каждом классе 10 образцов (всего 30 образцов). Очевидно, что первую часть мы будем использовать для обучения разных классификаторов, а вторую часть – для их проверки. Обучающую выборку мы будем называть Training, а проверочную Test. Классы называются в соответствие с их латинскими наименованиями: Setosa, Versicolor и Virginica, а переменные обозначаются двумя буквами, соответственно: SL – длина чашелистика (sepal length); SW – ширина чашелистика (sepal width), PL – длина лепестка (petal length), PW – ширина лепестка (petal width). Рис. 5 Статистические характеристики обучающего и проверочного наборов На Рис. 5 показаны основные статистические характеристики обучающего и проверочного наборов. Средние значения (m) каждой переменной (SL, SW, PL и PW) показаны точками, а их среднеквадратичные отклонения (s) – отрезками. Цвет значков соответствует классу: красный – Setosa, голубой – Versicolor и зеленый – Virginica. Форма значка соответствует набору, которому принадлежит образец: круг – обучающий набор, треугольник – проверочный набор. Мы и в дальнейшем будем использовать эту систему обозначений на графиках. Из Рис. 5 видно, что переменные в разных классах отличаются как по m, так и по s. Кроме того, мы можем заключить, что разбиение на обучающий и проверочный наборы было сделано правильно – соответствующие графики похожи. 2.3. Рабочая книга Iris.xlsЭто пособие сопровождает файл Iris.xls – рабочая книга Excel Эта книга включает в себя следующие листы: Intro: – краткое введение Data: – данные, используемые в примере. PCA – PCA декомпозиция данных PCA-LDA – Линейный дискриминантный анализ сжатых данных LDA – Линейный дискриминантный анализ полных данных QDA – Квадратичный дискриминантный анализ PLSDA – PLS дискриминация PLSDA-PCA-LDA – Линейный дискриминантный анализ результатов PLS дискриминации SIMCA_1 – SIMCA дискриминация первого класса SIMCA_2 – SIMCA дискриминация второго класса SIMCA_3 – SIMCA дискриминация третьего класса KNN – k ближайших соседей PCA-Explore – Кластеризация с помощью PCA kMeans – Кластеризация методом К-средних 2.4. Анализ данных методом главных компонентМетод главных компонент (PCA) – один из главных инструментов, применяемых в хемометрике. В задачах классификации он используется с двумя целями. Во-первых, PCA понижает размерность данных, заменяя многочисленные переменные на небольшой набор (обычно 2-5) главных компонент. Во-вторых, он служит основой для построения многих методов классификации, например метода SIMCA, который рассмотрен ниже. В рассматриваемом нами примере по классификации ирисов переменных немного – всего четыре, поэтому первая цель не столь важна. Тем не менее, мы построим PCA модель и посмотрим, насколько можно снизить эту размерность. PCA-анализ выполняется с помощью функций ScoresPCA и LoadingsPCA, PCA модель строится на обучающем наборе Xc и затем применяется к проверочному набору Xt. Из Рис. 5 следует, что данные необходимо центрировать, но не шкалировать. Графики первых счетов приведены на Рис. 6. Рис.6 Результаты PCA-анализа данных Графики старших компонент (PC3 – PC4) приведены здесь. Для того, чтобы определить сколько главных компонент достаточно для моделирование данных, нужно исследовать график, на котором объясненная дисперсия (ERV) для обучающего и проверочного изображается в зависимости от числа главных компонент (PC). Рис.7 Графики объясненной (ERV) дисперсии остатков для обучающего и проверочного наборов Из Рис. 7 видно, что двух PC достаточно для моделирования данных – они объясняют 98% вариаций, как для обучающего, так и для проверочного наборов. 3. Классификация "с учителем"3.1. Линейный дискриминатный анализ (LDA)Линейный дискриминантный анализ или LDA (Linear Discriminant Analysis) это старейший из методов классификации, разработанный Р. Фишером, и опубликованный им в работе, которую мы уже упоминали выше. Метод предназначен для разделения на два класса. Обучающий набор состоит из двух матриц X1 и X2, в которых имеется по I1 и I2 строк (образцов). Число переменных (столбцов) одинаково и равно J. Исходные предположения состоят в следующем:
Классификационное правило в LDA очень простое – новый образец x относится к тому классу, к которому он ближе в метрике Махаланобиса
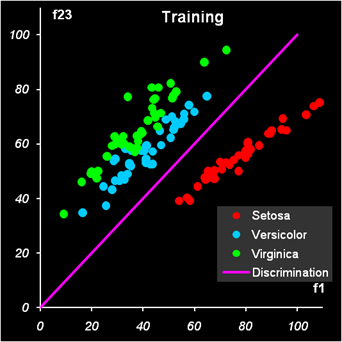
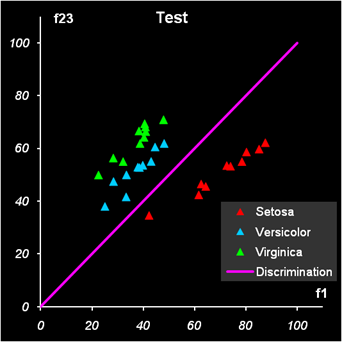
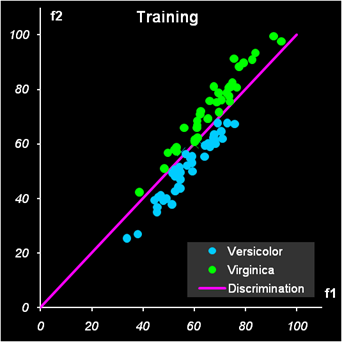
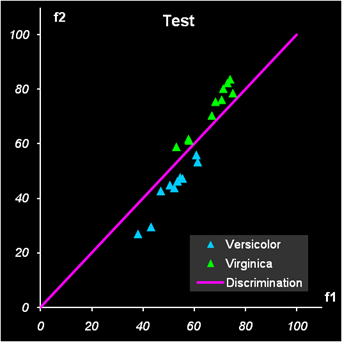
В этих формулах
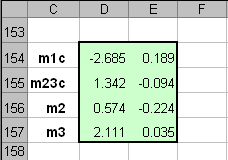
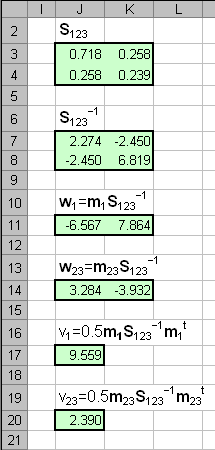
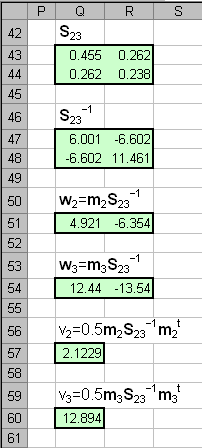
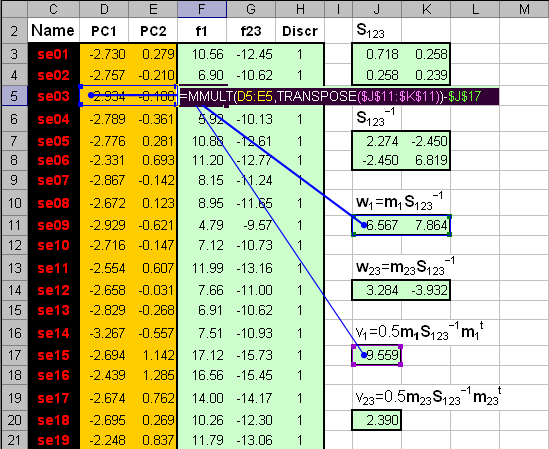
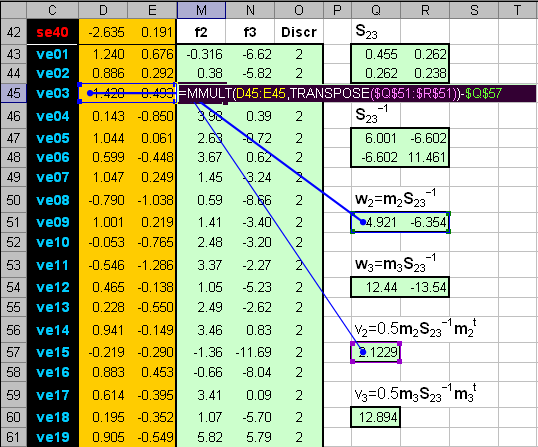
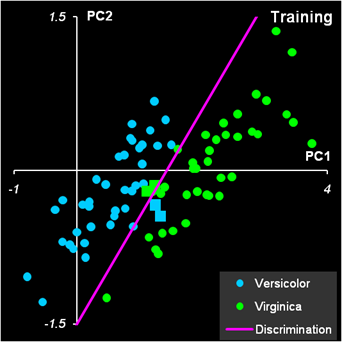
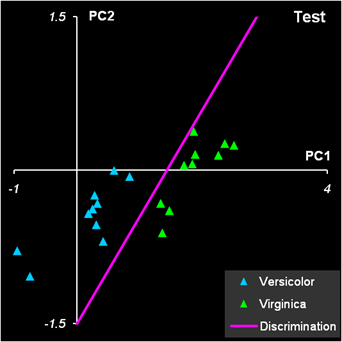
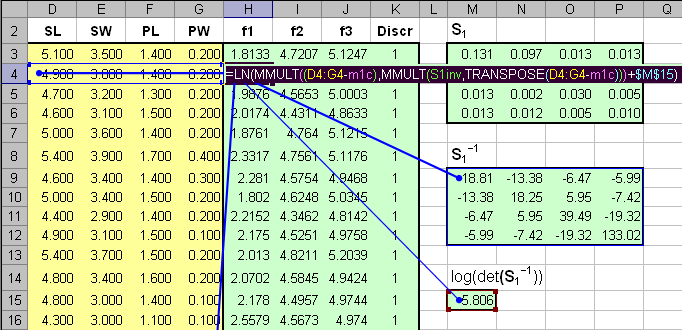
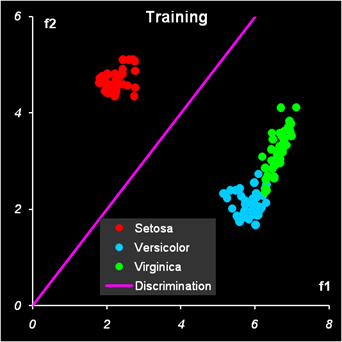
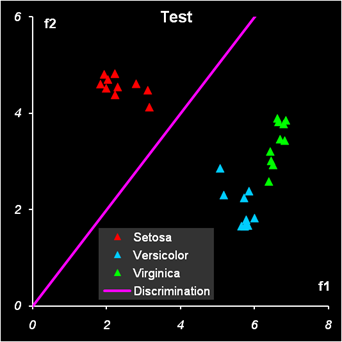
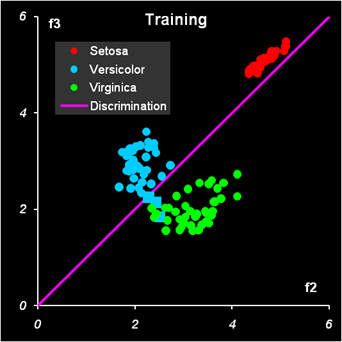
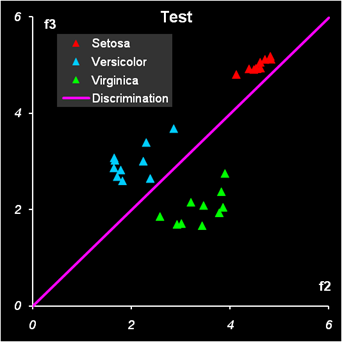
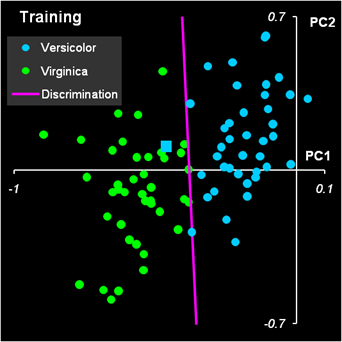
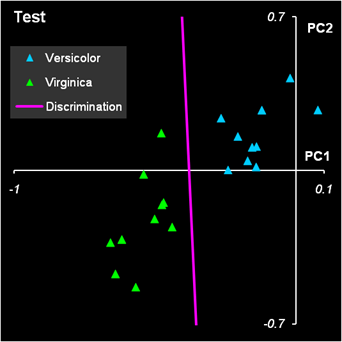
где Величины, стоящие в разных частях уравнения (4) называются LDA-счетами, f1 и f2. Образец относится к классу 1, если f1 > f2 , и, наоборот, к классу 2, если f1 < f2. Главной проблемой в методе LDA является обращение матрицы S. Если она вырождена, то метод использовать нельзя. Поэтому часто, перед применением LDA, исходные данные X заменяют на матрицу PCA-счетов T, которая уже не вырождена. Покажем, как LDA работает на примере классификации ирисов. Для большей иллюстративности мы сначала применим PCA, а уже потом LDA. Из раздела 2.4 ясно, что двух главных компонент будет достаточно. Т.к. LDA – это двухклассовый дискриминатор, то мы проведем классификацию в два шага. Сначала построим классификатор, который отделяет класс 1 (Setosa) от всех других ирисов, объединенных в класс 23 (Versicolor + Virginica). Затем построим второй классификатор, разделяющий классы 2 (Versicolor) и 3 (Virginica). Вычисления показаны на листе PCA-LDA. Начнем с вычисления средних значений для всех классов по обучающим наборам. Нам надо вычислить средние значения по классу 1 (I1=40), объединенному классу 23 (I23=80), и классам 2 (I2=40) и 3 (I3=40). Значения приведены в массивах с локальными именами: m1c, m23c, m2c и m3c. . Рис.8 Расчет средних значений Вычислим ковариационные матрицы, составленные из классов 1 и 23, а также из классов 2 и 3 и обратим их. Результаты представлен в массивах с локальными именами Sinv123 и Sinv23. Используя формулы (5) вычислим все необходимые нам величины . Рис.9 Расчет матриц ковариациий и других параметров LDA Теперь, используя формулу (4), мы можем рассчитать LDA-счета f1 и f23 и определить принадлежность всех образцов к классам 1 и 23. . Рис.10 Расчет LDA-счетов и принадлежности к классам 1 и 23 Аналогично проводится расчет для разделения классов 2 и 3. . Рис.11 Расчет LDA-счетов и принадлежности к классам 2 и 3 Результат первой дискриминации между классами 1 и 23 показан на Рис. 12. Рис.12 Результат первой дискриминации между классами 1 и 23 Дискриминационная прямая (4) безошибочно разделяет классы как в обучающем, так и в проверочном наборе. Рис.13 Результат второй дискриминации между классами 2 и 3 Результат второй дискриминации между классами 2 и 3 представлен на Рис. 13. Здесь есть ошибки в обучении: два образца из класса 2 ошибочно отнесены к классу 3, и также два образца из класса 3 ошибочно отнесены к классу 2. Эти точки показаны квадратными значками. В проверочном наборе ошибок нет. В примере с ирисами переменных мало, ковариационные матрицы невырождены, поэтому можно построить LDA классификацию и без предварительного использования PCA. Соответствующие расчеты представлены на листе LDA. Рис.14 Результат первой дискриминации между классами 1 и 23 На Рис. 14 и Рис. 15 показаны результаты LDA классификации. Рис.15 Результат второй дискриминации между классами 2 и 3 Т.к. переменных теперь не две, а четыре, то графики, иллюстрирующие результаты, можно построить только в координатах LDA-счетов (f1, f2) и дискриминирующая прямая - это биссектриса f1 = f2 первого квадранта. Вторая дискриминации в обучающем наборе проведена с ошибками: два образца из класса 2 ошибочно отнесены к классу 3, и один образец из класса 3 ошибочно отнесен к классу 2. Эти точки показаны квадратными значками. В проверочном наборе ошибок нет Недостатки LDA.
Достоинства LDA:
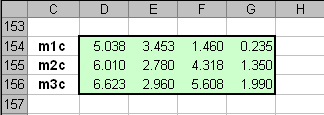
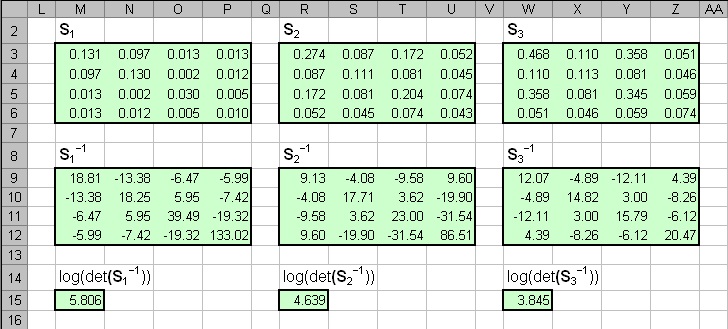
3.2. Квадратичный дискриминатный анализ (QDA)Квадратичный дискриминантный анализ, QDA (Quadratic Discriminant Analysis) является естественным обобщением метода LDA. QDA– многоклассный метод и он может использоваться для одновременной классификации нескольких классов k=1,…, K. Обучающий набор состоит из K матриц X1 ,…, XK, в которых имеется I1 ,…, IK строк (образцов). Число переменных (столбцов) одинаково и равно J. Сохраняя первое предположение LDA в (1), откажемся от второго, т.е. допустим, что ковариационные матрицы в каждом классе различны. Тогда QDA-счета вычисляются по формуле Классификационное правило QDA такое – новый образец x относится к тому классу, для которого QDA-счет наименьший. На практике, также как и в LDA, неизвестные математические ожидания и ковариационные матрицы заменяются их оценками В этих формулах
fk = fl поэтому метод и называется квадратичным. Рассмотрим, как метод QDA применяется к задаче классификации ирисов. Все расчеты приведены на листе QDA. Обучающий массив состоит из трех классов (с локальными именами X1c, X2c, X3c), по 40 образцов в каждом. Для каждого массива вычисляются средние значения (локальные имена m1c, m2c и m3c) . Рис.16 Расчет средних значений Потом вычисляются и обращаются ковариационные матрицы (локальные имена Sinv1, Sinv2 и Sinv3 . Рис.17 Расчет матриц ковариаций После этого можно рассчитать QDA счета и определить принадлежность к классам. Рис.18 Расчет QDA-счетов и принадлежности к классам Результаты классификации представлены графиками QDA-счетов, показанными на Рис. 19 . Рис.19 Результаты QDA классификации Из этих рисунков (а также из анализа QDA-счетов) видно, что классификация в обучающем наборе проведена с ошибками: три образца из второго класса (Versicolor) отнесены к третьему (Virginica). В проверочном наборе ошибок нет. Квадратичный дискриминантный анализ сохраняет большинство недостатков LDA.
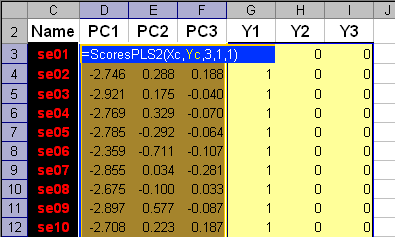
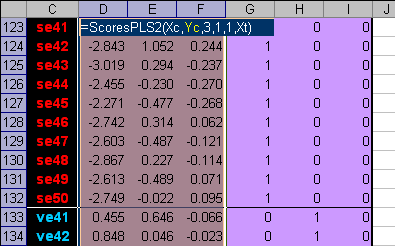
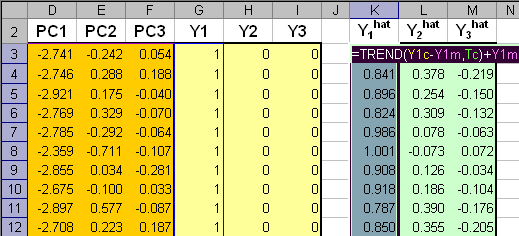
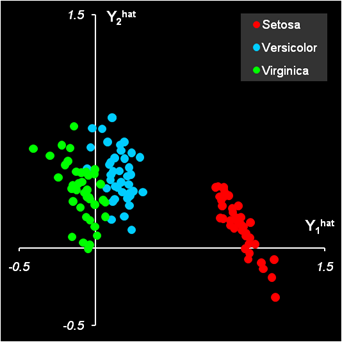
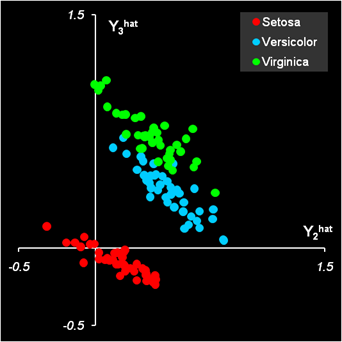
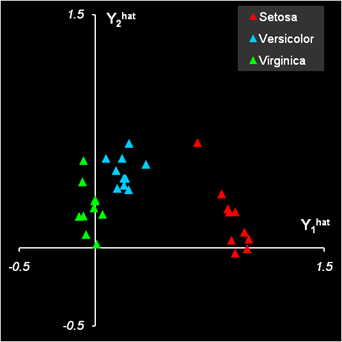
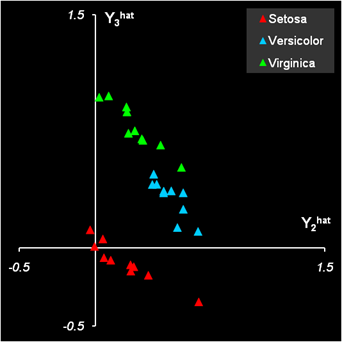
3.3. PLS дискриминация (PLSDA)Мы уже отмечали, что между задачами классификации и калибровки есть много общего. Метод PLS дискриминации, PLSDA (PLS-Discriminant Analysis) основан на этом принципе. Будем рассматривать имеющиеся у нас данные как набор предикторов (обучающий Xc и проверочный Xt). Дополним их фиктивными (dummy) матрицами откликов – обучающей Yc и проверочной Yt. – которые формируются по следующему правилу. Число предикторов (столбцов) в матрицах Y должно быть равно числу классов (в нашем случае – три). В каждой строке матрицы Y должны стоять нули (0) или единицы (1) в зависимости от того, к какому классу относится эта строка – если строка соответствует k-ому классу, то в k-ом столбце должна стоять 1, в остальных столбцах нули. Пример такой матрицы приведен на листе PLSDA (области с локальными именами Yc и Yt). Между блоком предикторов Xc и блоком откликов Yc строится PLS2-регрессия , и по ней вычисляются предсказанные значения фиктивных откликов Yhat для обучающего и проверочного наборов. Для нового образца x вычисляется PLS2 прогноз, т.е. строка новых откликов y1,…yK . Классификационное правило в PLSDA такое – образец принадлежит к тому классу, для которого соответствующий элемент yk ближе к единице. Практически определяется индекс k на котором достигается Применение PLSDA в задаче классификации ирисов показано на листе PLSDA. Расчеты начинаются с формирования матрицы фиктивных откликов и вычисления PLS2-счетов. Рис.20 Построение PLS2 регрессии Заметим, что при получении PLS2-счетов для проверочного набора используется несколько другая формула. Для вычисления прогнозных значений откликов Yhat применяется функция ТЕНДЕНЦИЯ (TREND). В версии Excel 2003 эта функция иногда дает неправильный результат. Чтобы предотвратить эту ошибку, мы используем центрированные значения фиктивных откликов в обучающем наборе . Рис.21 Расчет прогноза фиктивных откликов Результаты PLSDA классификации на обучающем наборе таковы: 15 образцов из второго класса (Versicolor) ошибочно отнесены к третьему классу (Virginica), четыре образца из третьего класса (Virginica) ошибочно отнесены ко второму классу (Versicolor). В проверочном наборе тоже есть ошибки: один образец из первого класса ошибочно отнесен ко второму, и два образца из второго класса ошибочно отнесены к третьему классу. Таким образом, мы можем заключить, что PLSDA классификация удовлетворительных результатов не дала. Однако ситуацию можно значительно улучшить, если отказаться от плохого правила классификации (8) и продолжить вычисления дальше. Рис.22 Результаты PLSDA классификации Будем рассматривать найденные величины прогнозных значений фиктивных откликов Yhat не как окончательные, а как промежуточные данные, и применим к ним какой-нибудь другой метод классификации, например LDA. Напрямую это сделать нельзя, поскольку матрица Ychat имеет ранг K–1, и матрицы ковариаций (3) будут вырождены. Поэтому, до применения LDA, необходимо использовать метод главных компонент (PCA), так же, как мы делали в разделе 3.1. Соответствующие вычисления приведены на листе PLSDA-PCA-LDA . Рис.23 Результаты PLSDA-PCA-LDA классификации Этим способом мы получаем результат, в котором имеется всего одна ошибка в обучении: один образец из второго класса (Versicolor) ошибочно отнесен к третьему классу (Virginica). В проверочном наборе ошибок нет. В этом методе PLS2-регрессия на матрицу фиктивных откликов с последующей PCA проекцией (PLSDA-PCA) является предварительной подготовкой исходных данных X, т.е. некоторым фильтром, выявляющим в этих данных новые характеристики, непосредственно связанные с различиями между классами. Здесь принципиально важно, что в PCA-LDA метод применяется к матрице предсказанных фиктивных откликов Yhat, не к матрице PLS2-счетов. Недостатки PLSDA
Достоинства PLSDA
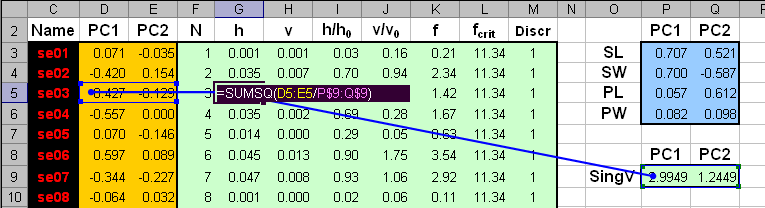
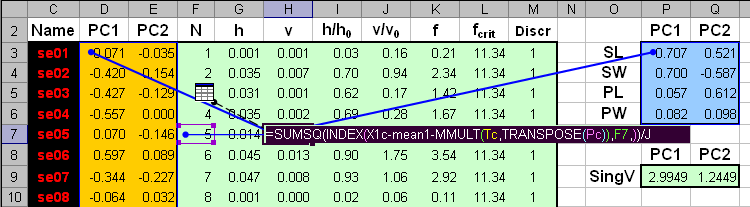
3.4. SIMCAВ этом разделе мы рассмотрим метод с длинным названием Формальное независимое моделирование аналогий классов, или, сокращенно, SIMCA (Soft Independent Modeling of Class Analogy). Уникальность этого метода определяется несколькими особенностями. Во-первых, каждый класс моделируется обособленно, независимо (independent) от остальных. Поэтому SIMCA является одноклассовым методом. Во-вторых, SIMCA классификация является многозначной (soft) – каждый образец может быть одновременно отнесен к нескольким классам. В-третьих, в SIMCA есть уникальная возможность установить значение ошибки 1-го рода и построить соответствующий классификатор. В методах, рассмотренных выше, ошибки 1-го и 2-го рода возникают как данность, изменить которую невозможно. Например, в LDA ошибки 1-го рода (α) и 2-го рода (β) можно (с большим трудом) вычислить, но изменить нельзя. Т.к. SIMCA является одноклассовым методом, то, при его объяснении мы будем рассматривать только один класс, представленный матрицей X, размерностью I образцов и J переменных. Наша цель – построить такое классификатор (правило), по которому любой новый образец x либо принимается как принадлежащий тому же классу, что и X, либо отвергается. Для решения этой задачи представим матрицу X как облако из I точек в J-мерном пространстве свойств. Начало координат этого пространства мы поместим в центр тяжести этого облака. Заметим, что форма облака часто является специфичной – из-за сильной корреляции между свойствами, точки могут быть расположены близко к некоторой гиперплоскости (подпространству), имеющей эффективную размерность A<J. Для определения построения этой гиперплоскости и определения размерности A применяется метод главных компонент. Каждый элемент данных можно представить как сумму двух векторов: лежащего в найденной гиперплоскости (проекция) и перпендикулярного гиперплоскости (остаток). Длины этих векторов являются важными показателями, характеризующими принадлежность точки к классу. Они называются, соответственно, размахом h и отклонением v. Как только появляется новая точка – кандидат на принадлежность к классу – ее можно спроецировать на уже имеющееся подпространство и определить ее собственные характеристики: размах и отклонение. Сравнивая эти величины с критическими уровнями, определенными по обучающему набору, можно принять решение о принадлежности нового наблюдения к классу. .
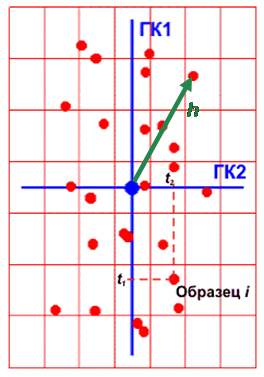
Рис.24 Размах и отклонение в PCA Пусть построена PCA декомпозиция обучающей матрицы X X = TPt + E Тогда каждый образец x (обучающий, проверочный или новый) может быть спроецирован на пространство PC, т.е. найден вектор его счетов t=xP=(t1,…,tA)t Размах h вычисляется по следующей формуле где sa – это
сингулярные значения,
т.е.
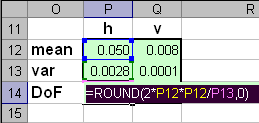
Разница между исходным вектором x и его декомпозицией является остатком. Отклонение v – это среднеквадратичный остаток Существуют веские основания считать, что каждая из величин h и v подчиняется распределению хи-квадрат, точнее где h0 и v0 – это средние значения величин h и v, а Nh, и Nv – это числа степеней свободы соответственно для h и v. Используя обучающий набор Xc=(x1,…xI)t, можно найти I значений размахов h1,….,hI и отклонений v1,….,vI. По ним можно оценить соответствующие средние значения После этого числа степеней свободы Nh, и Nv определяются с помощью метода моментов Статистика f, по которой проводится классификация, вычисляется по формуле Из (12) следует, что
Пусть α – это заданная величина ошибки 2-го рода (ложное отклонение образца, который принадлежит классу). Обозначим где
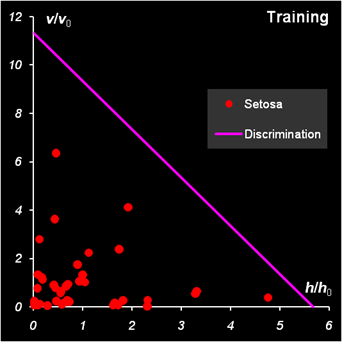
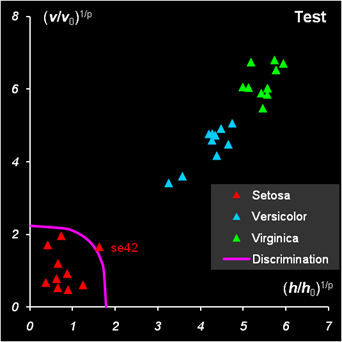
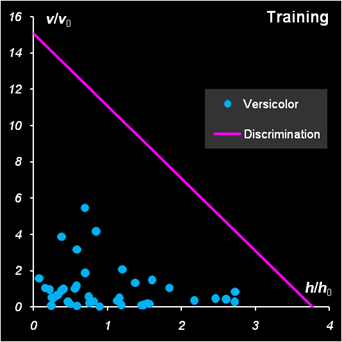
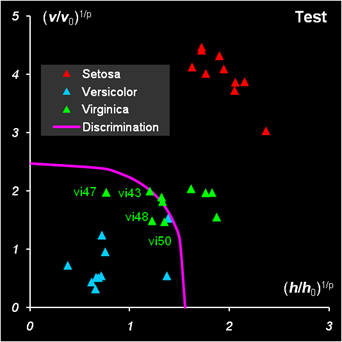
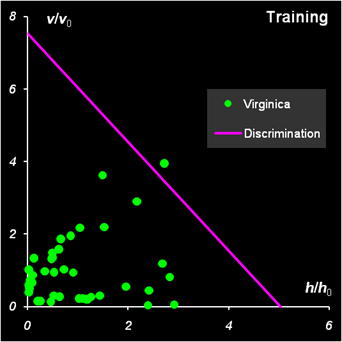
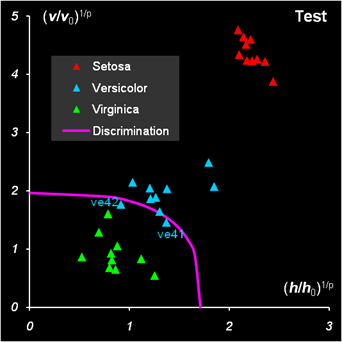
Классификационное правило в методе SIMCA такое – образец принимается как принадлежащий к классу, если f < fcrit Этим правилом гарантируется, что (1-α)100% образцов из обучающего и проверочного наборов будут правильно классифицированы. Рассмотрим, как метод SIMCA применяется в задаче классификации ирисов. Начнем с первого класса (Setosa) и построим для него одноклассовый SIMCA классификатор. Расчеты приведены на листе SIMCA_1. Первым делом применим PCA, используя в качестве обучающего набора матрицу X1c (часть матрицы Xc относящуюся к классу 1), а в качестве проверочного набора всю матрицу Xt. Также как и в других методах, мы используем две PCA компоненты. Рис.25 Вычисление счетов и нагрузок PCA Области, в которых находятся значения счетов (обучающих и проверочных) и нагрузок, имеют локальные имена Tc, Tt и Pc. После этого можно вычислить сингулярные значения, суммируя квадраты счетов для каждой PC, и затем извлекая корень из результата. Затем вычисляем значения размахов h по формуле (9) для обучающего и проверочного наборов. . Рис.26 Вычисление размахов Отклонения v вычисляются несколько сложнее. Здесь мы комбинируем (10) и (11) способом описанным здесь. . Рис.27 Вычисление отклонений Вычисление отклонений для проверочного набора проводится по аналогичной формуле с заменой X1c на Xt, и Tc на Tt. Когда величины h и v получены, можно найти их средние значения (13) и дисперсии (14), а потом оценить числа степеней свободы по формулам (15). Рис.28 Вычисление числа степеней свободы Теперь можно вычислить значения статистики f (16). Зададим величину α= 0.01. В дальнейшем ее можно менять и наблюдать изменения в результатах классификации. Величина критического уровня fcrit вычисляется по формуле (17). Рис.29 Вычисление числа степеней свободы Здесь используется стандартная функция Exсel CHIINV (ХИ2ОБР). Рис.30 Вычисление числа степеней свободы На Рис. 30 показаны результаты классификации. График для проверочного набора модифицирован так, чтобы показать на нем все имеющиеся образцы. Для этого оси координат трансформированы степенным преобразованием x1/p, p=3. Все образцы обучающего набора классифицированы правильно. В проверочном наборе один образец из первого класса (Setosa) не распознан. Аналогично делается классификация для других классов. При этом для класса 2 (лист SIMCA_2) обучающей является подматрица X2c, а для класса 3 (лист SIMCA_3) – подматрица X3c. Соответственно меняются и средние значения mean2 и mean3, необходимые для вычисления отклонений. Рис.31 Результаты SIMCA классификации для класса 2 Рис.32 Результаты SIMCA классификации для класса 3 Окончательные итоги SIMCA классификации таковы. Один образец из третьего обучающего набора не был принят (ошибка 1-го рода). В проверочных наборах один образец из первого класса не был классифицирован (ошибка 1-го рода), два образца из второго класса были одновременно отнесены и к третьему классу (ошибка 2-го рода), четыре образца из третьего класса были отнесены также и ко второму классу (ошибка 2-го рода). Актуальная ошибка 1-го рода получилась 2/150 ≈ 0.013, что близко к установленной α= 0.01. Недостатки SIMCA
Достоинства SIMCA
3.5. K ближайших соседей (KNN)Метод k ближайших соседей (k-Nearest Neighbors, kNN) – один из простейших методов классификации. Пусть, как и раньше, имеется обучающий набор Xc разбитый на классы, и новый неизвестный объект x, который надо классифицировать. Вычислим расстояния (обычно, эвклидово) от x до всех образцов обучающего набора (x1,…, xI) и выделим среди них k ближайших соседей, расстояние до которых минимально. Новый объект x принадлежит к тому классу, к которому относится большинство из этих k соседей. Параметр k подбирается эмпирическим путем. Увеличение k приводит к уменьшению влияния погрешностей, но ухудшает разделение на классы. Покажем, как метод kNN работает в задаче о разделении ирисов. Рассчитаем расстояния от каждого проверочного образца до всех образцов обучающего набора. Для этого составим таблицу, показанную на листе kNN. Строки этой таблицы соответствуют обучающему набору, а столбцы – проверочному Рис.33. Расчет расстояний между образцами Для вычисления расстояний между образцами используются два глобальных имени nC и nT (лист Data), соответствующие наборам имен обучающих и проверочных образцов. После того, как все расстояния вычислены, каждый столбец фильтруется с упорядочиванием по возрастанию расстояний, так, чтобы наименьшие оказались вверху. Остальное уже просто – надо только просмотреть все столбцы, и определить, к какому классу относятся проверочные образцы. Рис.34. Семь ближайших соседей для проверочных образцов В результате все образцы оказались правильно классифицированы. Недостатки kNN.
Достоинства
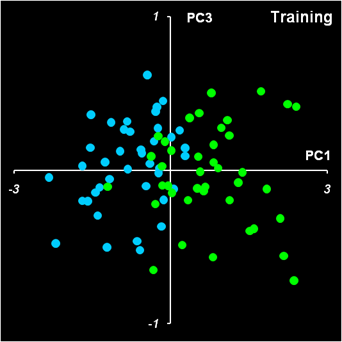
4. Классификация без учителя4.1. Опять PCAМетод главных компонент является простейшим и наиболее популярным методом классификации без обучения. Для его исследования мы будем использовать только обучающий набор, исключив проверочный из рассмотрения. Вычисления приведены на листе PCA-Explore. Теперь мы заранее не знаем, к какому из классов принадлежат образцы и, более того, даже число классов нам неизвестно. Рис.35. PCA анализ обучающего набора Однако, рассматривая график PCA-счетов для всего обучающего набора, мы легко можем выделить группу образцов (обведенную эллипсом), которая явно отделяется от всех прочих объектов. Естественно предположить, что эти образцы принадлежат к отдельному классу. Удалим все эти образцы из обучающего набора и применим PCA к оставшимся образцам. На графике PC1-PC2 счетов, показанных на Рис. 36 можно (при большом воображении) различить два кластера, показанные эллипсами. Но уже на графике старших счетов PC1-PC3, мы ничего похожего на классы не видим. Рис.36. PCA анализ укороченного обучающего набора Таким образом, исследование данных с помощью PCA может выявить скрытые классы, а может, и нет. В любом случае необходима дальнейшая проверка этих гипотез с помощью других методов классификации без учителя. 4.2. Кластеризация с помощью K-средних (kMeans)Существует большой класс методов, выполняющих так называемую кластеризацию. Кластеризация состоит в том, чтобы разделить образцы на подмножества (называемые кластерами) так, чтобы все образцы в одном кластере были в каком-то смысле похожи друг на друга. Оценка схожести образцов x1и x2 обычно основана на анализе расстояний d(x1, x2) между ними. Для измерения расстояний чаще всего используют Эвклидову метрику. Самым простым (и поэтому – популярным) является метод K-средних (K-means). Этот метод разбивает исходный набор образцов на заранее известное число K кластеров. При этом каждый образец xi обязательно принадлежит к одному из этих кластеров Sk., k=1,…, K. Каждый кластер k характеризуется своим цетнроидом mk – точкой, являющейся центром масс всех образцов кластера. Метод K-средних – это итерационный алгоритм, в котором на каждом шаге выполняются следующие операции. 1. Определяются расстояния от всех образцов до центроидов d(xj, mk), j=1,…J; k=1,…,K . 2. Образцы относятся к кластерам в соответствии с тем, какой из центроидов оказался ближе. 3. По этому новому разбиению вычисляются центроиды mk для каждого из кластеров
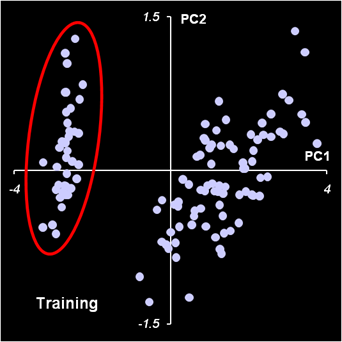
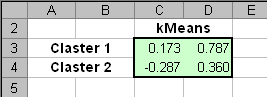
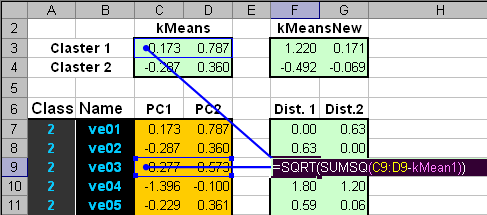
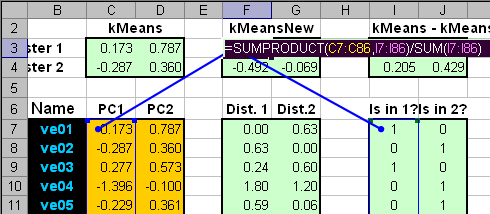
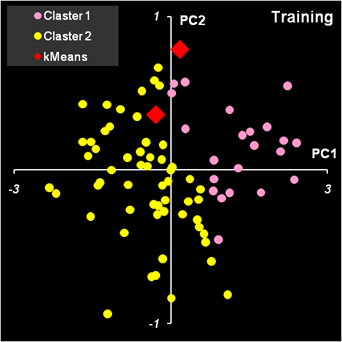
где Jk – это число образцов в кластере Sk. Операции 1-3 повторяются до сходимости. Для инициализации алгоритма нужно задать исходные значения всех центроидов mk. Это можно сделать произвольно, например, положить их равными первым K образцам. m1= x1, m2= x2,…., mK= xK Покажем, как метод K-средних работает в примере с ирисами. Полный набор данных весьма громоздкий, да и первый класс (Setosa) легко отделяется от остальных методом PCA. Поэтому мы будем анализировать только укороченный обучающий набор из первых двух PC, показанный на Рис. 36. На листе kMeans приведен набор PCA счетов соответствующий двум первым PC для укороченного обучающего набора (классы 2 и 3). Естественно, что мы будем проводить анализ для двух классов (K=2). Текущие значения двух центроидов приведены в областях с локальными именами kMean1 и kMean2. Их начальные значения соответствуют первым двум образам. Рис.37. Начальные значения центроидов Расстояния от всех образцов до двух центроидов (шаг 1) вычисляются в Эвклидовой метрике Рис.38. Вычисление расстояний до центроидов После этого определяется, к какому кластеру принадлежит каждый образец (шаг 2). Рис.39. Определение принадлежности образцов к кластерам После этого, в новом месте листа, рассчитываются новые значения центроидов (шаг 3) Рис.40. Расчет новых значений центроидов Чтобы замкнуть итерационную последовательность надо скопировать значения из области KMeansNew и вставить их (как значения!) в область KMeans. И это надо повторять столько раз, сколько потребуется, пока все значения kMeans – kMeansNew не станут равными нулю. На листе kMeans имеется кнопка Calculate. Она запускает простейший VBA макрос, который копирует содержание области KMeansNew и вставляет значения в область KMeans. Эта операция повторяется столько раз, сколько указано в клетке P2. Тем самым реализуется заданное число итераций. Итерационная процедура всегда сходится, но результат может быть разным, в зависимости от выбора начальных центроидов. Если выбрать в качестве начального приближения первые две точки: ve01 и ve02 , то получится результат, представленный на Рис. 41. Левый график показывает, как образцы распределялись в начале работы алгоритма, а правый график – как они распределились в итоге.
Рис.41. Кластеризация методом K-средних. Начало и
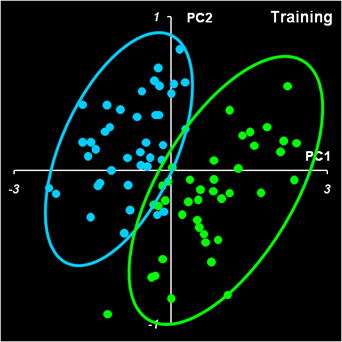
конец работы алгоритма. На Рис. 42 показан результат кластеризации, который получается, если в качестве начального приближения берутся последние два образца: vi39 и vi40. Во-первых, видно, что кластеры поменялись местами. Во-вторых, заметно, что некоторые точки ушли в другие кластеры.
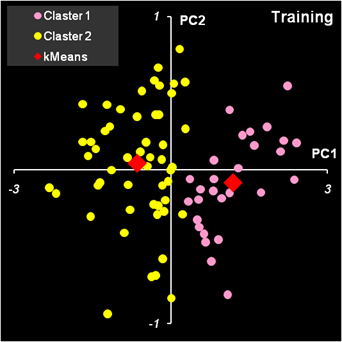
Рис.42. Кластеризация методом K-средних. Начало и
конец работы алгоритма. Для того, чтобы понять какое решение лучше, используют целевую функцию
которая должна быть минимальна. В первом случае S=52.830, а во втором S=52.797. Таким образом, второе решение предпочтительнее. Естественно отождествить первый кластер с классом 2 (Versicolor), а второй кластер с классом 3 (Virginica). Тогда полученные результаты можно интерпретировать так: два образца класса 2 идентифицированы неправильно, а среди образцов класса 3 одиннадцать неверно отнесены к классу 2. Метод K-средних имеет несколько недостатков.
ЗаключениеМы рассмотрели некоторые методы, используемые для решения задач классификации. Эта область хемометрики, как никакая другая, изобилует разнообразными подходами. Поэтому, с неизбежностью, за рамками этого пособия остались многие интересные методы, такие как, например, UNEQ, CART и другие. Разобраться с тем, как они работают можно самостоятельно, используя это пособие как руководство к действию. Несколько методов классификации достойны специального изучения. Это методы опорных векторов и искусственных нейронных сетей. Им будут посвящены отдельные пособия
|