Кинетическое моделирование спектральных данных
- © 2010 Алексей Померанцев
Содержание
- Введение
- Метод "серого" моделирования
- 1 Постановка задачи
- 2. Пример
- 3. Данные
- 4. Формальный метод чередующихся наименьших квадратов (Soft-ALS)
- 5. Содержательный метод чередующихся наименьших квадратов (Hard-ALS)
- 6. Использование надстройки Solver
- Заключение
Введение
В этом небольшом пособии рассмотрены кинетические методы, применяемые для решения задач разрешения многомерных кривых (multivariate curve resolution). Текст ориентирован, прежде всего, на специалистов в области анализа экспериментальных данных: химиков, физиков, биологов, и т.д. Он может служить пособием для исследователей, начинающих изучение этого вопроса. Продолжить исследования можно с помощью указанной литературы.
В пособии интенсивно используются понятия и методы, описанные в других материалах по хемометрике: матричная алгебра, разрешение многомерных кривых . Читателям, которые плохо знакомы с этим аппаратом, рекомендуется изучить, или, хотя бы просмотреть, эти материалы.
Изложение иллюстрируется примерами, выполненными в рабочей книге Excel “Grey.xls”, которая сопровождает этот документ.
Важная информация о работе с файлом Grey.xls
Предполагается, что читатель имеет базовые навыки работы в среде Excel, умеет проводить простейшие матричные вычисления с использованием функций листа, таких как МУМНОЖ, ТЕНДЕНЦИЯ и т.п. В отличие от других пособий из серии, здесь не используется надстройка Chemometrics Add-In, зато применяется стандартная надстройка Solver.
Метод "серого" моделирования
1. Постановка задачи
Исходная постановка задачи аналогична рассмотренной в пособии "Многомерное разрешение кривых (MCR)". Рассматривается система, состоящая из нескольких веществ (компонент), A, B, … , концентрации которых cA(t), cB(t),… закономерно изменяются со временем t, подчиняясь известному кинетическому механизму. С другой стороны каждый компонент может быть охарактеризован своим чистым спектром (понимаемым в обобщенном виде): sA(λ), sB(λ),…., где λ – это длина волны. По ходу эксперимента, в момент времени ti, на длине волны λj измеряется величина
x(ti, λj)=cA(ti) sA(λj)+cB(ti) sB(λj)+ ....
равная линейной суперпозиции всех спектров и концентраций "чистых" компонентов.
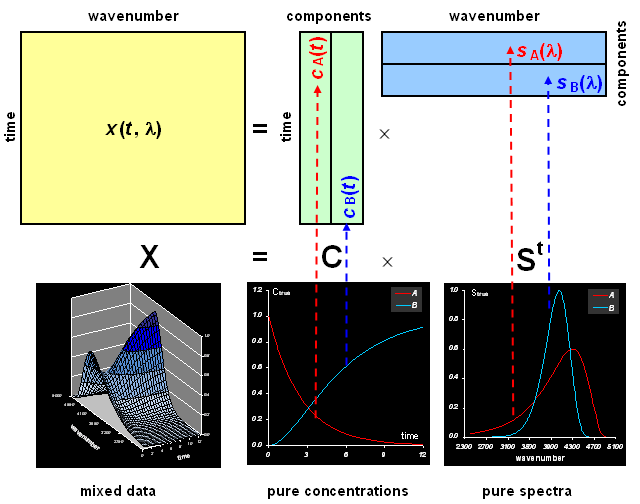
Рис. 1 Устройство спектрально-кинетических данных
Пусть I – это число моментов наблюдений: t1,….tI, а J – это число длин волн λ1,…,λJ. Тогда данные, получаемые в эксперименте, можно представить в матричном виде
|
(1) |
Здесь матрицы данных X и погрешностей E имеют размерность I×J . Если в системе присутствует A химических компонентов, то матрица концентраций C имеет I строк и A столбцов. Каждый ее столбец – это кинетический профиль изменения концентрации соответствующего вещества. Матрица чистых спектров St (ее удобнее представлять в транспонированном виде) имеет A строк и J столбцов. Каждая ее строка – это чистый спектр соответствующего компонента.
Задача MCR состоит в том, чтобы по заданной матрице данных X найти матрицы концентраций C и чистых спектров S. Для ее решения можно применять обычные, формальные (soft) методы, описанные в пособии Разрешение многомерных кривых. Однако, в отличие от общей задачи MCR, в рассматриваемом случае нам известны кинетики изменения концентрации всех компонентов
cA(t)
= fA(t,
k1, ... , kp )
cB(t)
= fB(t,
k1, ... , kp )
...
но только с точностью до неизвестных кинетических параметров k =(k1, ... , kp ) – констант скоростей соответствующих реакций. Относительно матрицы спектров S известны только самые общие априорные сведения: неотрицательность, непрерывность, и т.п.
В такой постановке задача MCR является обратной задачей химической кинетики – определение оценок кинетических параметров для известного механизма при наличии "мешающих" параметров – спектральных величин (коэффициентов экстинкции). Обычно в традиционной обратной задаче исходными экспериментальными данными являются концентрации некоторых компонентов кинетической схемы, а не спектры.
В этом пособии мы покажем, как для решения спектральной задачи применяется метод "серого" моделирования, в котором сочетаются формальные ("черные") алгоритмы для оценки спектральных компонент S и содержательные ("белые") методы для оценки кинетических профилей C. Заметим, что для этого метода решение задачи MCR (если оно существует) является единственным.
2. Пример
Для иллюстрации и сравнения различных методов разделения кривых будем использовать модельный пример, помещенный в рабочую книгу Grey.xls.
Эта книга включает в себя следующие листы:
Intro: краткое введение
Layout: схемы, объясняющая имена массивов, используемых в примере
Kinetics: истинные концентрационные профили C
Spectra: истинные чистые спектры S
Data: модельные данные, используемые в примере. Oшибки формируются случайным образом на этой же странице.
Soft: формальный метод чередующихся наименьших квадратов (Soft-ALS)
Hard: содержательный метод чередующихся наименьших квадратов (Hard-ALS)
3. Данные
Прообразом для этого примера служит задача оценки кинетических параметров в последовательной реакции первого порядка
![]()
Эта кинетическая схема описывается системой дифференциальных уравнений
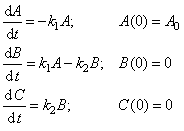
имеющих явное решение
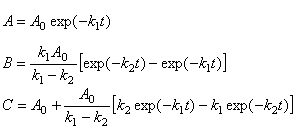 |
(2) |
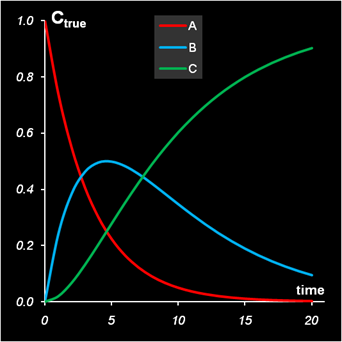
представленное на Рис. 2 для A0=1, k1=0.30, k2=0.15.
Рис. 2 Новая книга Excel
Эти кинетические профили вычисляются по формулам (2) на листе Kinetics для значений параметров k1и k2 заданных в ячейках H3 (Rate1) и H4 (Rate2), соответственно
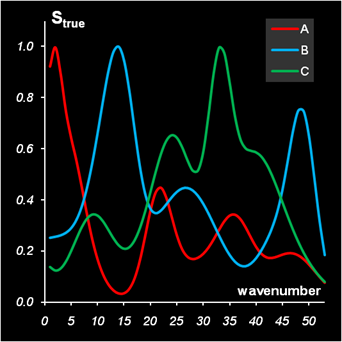
Для моделирования спектров использовались перекрывающиеся гауссовы пики, вычисленные для 53 условных длин волн. Они представлены на листе Spectra и показаны на Рис. 3.
Рис. 3 Спектры чистых компонент
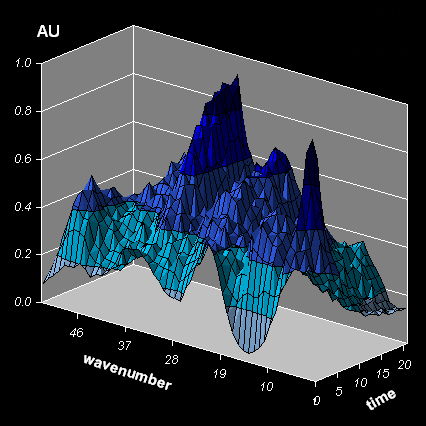
Смешанные данные X вычисляются на листе Data по формуле (1) с относительной ошибкой 5%. Величину этой ошибки (она задается в ячейке E27 с именем RMSE) можно менять и получать новые данные. Для этого нужно нажать кнопку Add New Error, запускающую VBA макрос MakeErrors, привязанный к этому листу.
Рис. 4 Модельные данные
4. Формальный метод чередующихся наименьших квадратов (Soft-ALS)
Для анализа полученных модельных данных X можно применить формальный метод чередующихся наименьших квадратов (ALS). Однако, в этом случае, стандартный алгоритм лучше уточнить, чтобы включить в него всю имеющуюся априорную информацию. Вот, что нужно учесть при построении метода.
1. Число компонент известно – их три: A, B, C;
2. Спектры неотрицательны;
3. Концентрации неотрицательны, причем A(0)=1, B(0)=C(0)=0;
4. Система замкнута, т.е. в любой момент t :
| A(t)+B(t)+C(t)=Const=1. |
(3) |
С учетом этой информации алгоритм метода выглядит так.
1. Задается окно – шаблон концентраций, в котором важны только нулевые значения, которые нужно удерживать при итерациях. В нашем случае, это: B(0)=C(0)=0.
2. Это окно используется как начальное приближение для матрицы концентрационных профилей Cin.
3. Из матрицы Cin создается матрица Cadj: элемент матрицы Cadj заменяется нулем, если соответствующий элемент Cin отрицателен, или если соответствующий элемент концентрационного окна равен нулю. Кроме того, матрица Cadj нормируется так, чтобы ее элемент (1,1) был равным 1, т.к. A(0)=1.
4. Для матрицы Cadj вычисляется сумма всех ее элементов по рядам и формируется вектор (Closure), отражающей замкнутость системы в соответствии с уравнением (3).
5. Из матрицы Cadj создается матрица Chat, удовлетворяющая условиям замкнутости. Для этого каждая строка матрицы Cadj делится на соответствующий элемент вектора Closure.
6. С помощью формулы
Sin= Xt Chat (ChattChat)–1
находится оценка матрицы чистых спектров Sin
6. Матрица Sin подправляется – отрицательные элементы заменяются нулями. Получается матрица Shat.
7. С помощью формулы
Cout=X Shat (ShattShat)–1
определяется оценка матрицы концентрационных профилей Cout.
8. Матрица Cin заменяется матрицей Cout
9. Шаги 3-8 повторяются до сходимости
Применение метода ALS для нашего примера показано на листе Soft. Здесь используется кнопка Calculate, которая запускает VBA макрос, копирующий содержание области Cout в область Cin. Число повторов задается значением в клетке K1 (имя iTer). Алгоритм сходится за 10 итераций к результату, который по точности (δ = 5%) совпадает с величиной использованной ошибки. Здесь δ – это относительная среднеквадратичная погрешность моделирования.
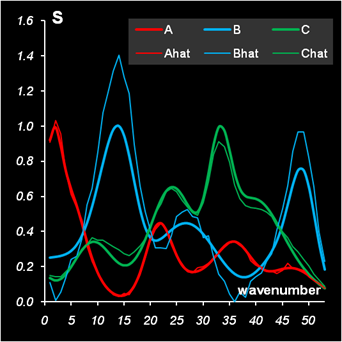
Рис. 5 Решение задачи методом формального ALS
Найденное решение показано на Рис. 5. Оно отличается от известных нам истинных значений. Разумеется, это следствие глобальной неоднозначности решения, найденного формальным методом
5. Содержательный метод чередующихся наименьших квадратов (Hard-ALS)
Применяя формальный метод ALS, мы никак не учитывали имеющееся у нас знание о форме кинетических профилей – модель кинетики изменения концентраций (2). Учет этой информации усложнит алгоритм, но, очевидно, улучшит анализ данных. Вот как выглядит этот новый алгоритм.
1. Задается начальное приближение для матрицы концентрационных профилей Cin, например как решение, полученное формальным методом ALS.
2. Задаются начальные значения кинетических параметров k1,…kp
3. Из матрицы Cin создается матрица Chat: элемент матрицы Chat заменяется нулем, если соответствующий элемент Cin отрицателен.
4. По известным уравнениям (2) вычисляются все концентрации, из которых формируется матрица Cfit.
5. Подбираются новые значения кинетических параметров k1,…kp такие, которые минимизируют величину
![]()
6. С помощью формулы
Sin= Xt Cfit (CfittCfit)–1
находится оценка матрицы чистых спектров Sin
7. Матрица Sin подправляется – отрицательные элементы заменяются нулями. Получается матрица Shat.
8. С помощью формулы
Cout=X Shat (ShattShat)–1
определяется оценка матрицы концентрационных профилей Cout.
9. Матрица Cin заменяется матрицей Cout
10. Шаги 3-9 повторяются до сходимости.
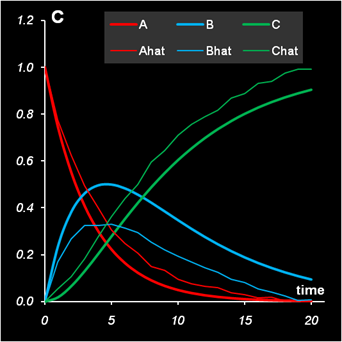
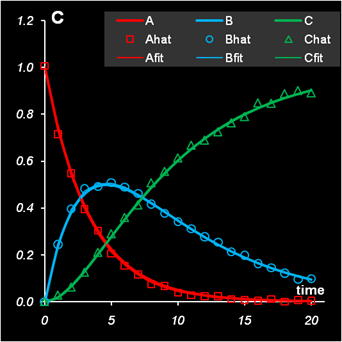
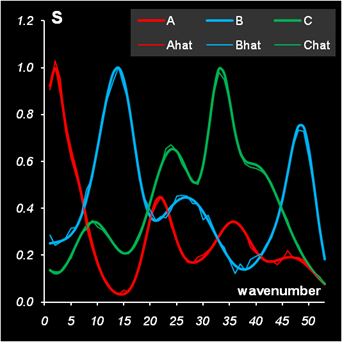
На Рис. 6 показаны решения модельной задачи, найденные с помощью описанного алгоритма.
Рис.6 Решение задачи методом содержательного ALS
Видно, что получилось гораздо лучше – ближе к истинным, исходным значениям концентраций и спектров. При этом глобальная ошибка стала несколько хуже, по сравнению с обычным ALS: 0.0200 против 0.0197. Условия замкнутости и положительности выполняются автоматически. От выбора начального приближения для матрицы Cin (шаг 1) сходимость зависит слабо.
6. Использование надстройки Solver
В описанном выше алгоритме наибольшую трудность представляет шаг 5 – подбор таких значений параметров k1 и k2,(заданных в ячейках Rates), которые минимизируют сумму квадратов разностей
||Chat – Cfit ||2
находящуюся в ячейке Fit.
Для этого мы используем процедуру Solver (Поиск решения) – стандартную надстройку Excel. Для ее подключения нужно следовать процедуре, описанной здесь, начиная со второй фазы
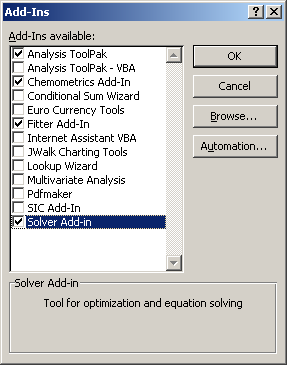
Рис.7 Подключение надстройки Solver
Вызывается Solver из меню (Excel 2003) или (Excel 2007). В появившемся диалоговом окне (Рис. 8) нужно указать параметры оптимизации: целевую величину и изменяемые параметры .
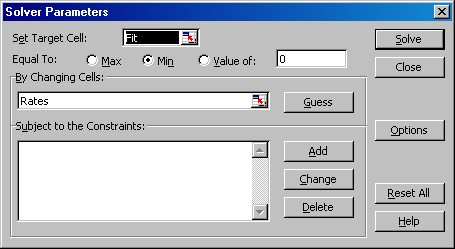
Рис.8 Надстройка Solver
Solver это не очень эффективный метод оптимизации, но если его настроить должным образом (так, как показано на Рис. 9), то поиск будет проходить быстро.
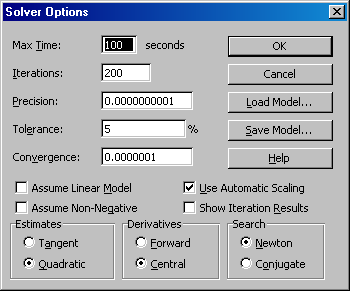
Рис.9 Настройка опций Solver
В целом, описываемый алгоритм – это довольно медленный метод. Например, для того, чтобы сойтись к решению из точки k1=0.5, k2 =0.1, требуется 300-400 итераций. Поэтому применять его на практике можно только в том случае, когда имеется некоторая автоматизация – кнопка Calculate, выполняющая заданное число итераций. Такая автоматизация возможна с применением стандартных функций надстройки Solver: SolverOptions, SolverOk, SolverSolve, описание которых приведено здесь.
Для того, чтобы VBA распознал и использовал эти функции, мало подключить надстройку Solver, необходимо также установить ссылку на библиотеку Solver в редакторе VBA. При попытке использовать встроенную автоматизацию (кнопка Calculate) без этой ссылки появится сообщение .
Рис.10 Ошибка ссылки
Для того, чтобы установить ссылку, надо зайти в редактор VBA и использовать меню . Появится окно, показанное на Рис. 11
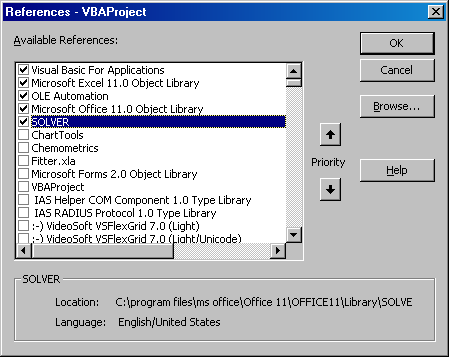
Рис.11 Установка ссылки на Solver
В этом окне нужно найти и поставить галочку напротив имени SOLVER.
В исходном файле Grey.xls , размещенном на нашем сервере, надстройка Solver не подключена и ссылка на нее в редакторе VBA отсутствует. Это сделано намерено, т.к. все установленные ссылки на надстройки являются специфичными для данного компьютера, и, будучи верными для нашего компьютера, они окажутся неверными при переносе файла на другой компьютер. Поэтому пользователь должен самостоятельно подключить Solver и установить ссылку на него в редакторе. Подробнее эта проблема Excel обсуждается здесь.
Заключение
Мы рассмотрели метод "серого" моделирования, применяемый для разрешения кинетических кривых, представленных спектральными данными. Эта новая, развивающаяся область хемометрики, в которой есть еще много белых пятен. Читателю предлагается самостоятельно исследовать возможности этого метода, меняя исходные модельные данные: параметры k1и k2 (лист Kinetics) , и ошибки (лист Data).