Проекционные методы в системе Excel
Содержание
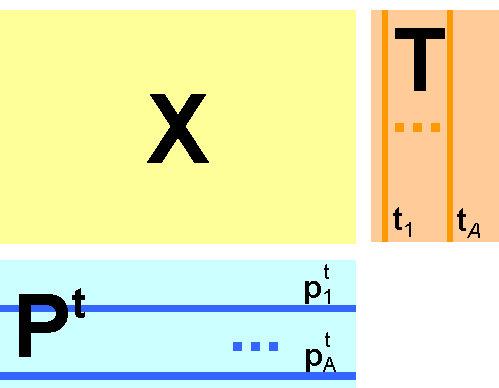
ВведениеВ этом пособии рассказывается о применении программного средства Chemometrics Add-In - специальной надстройки для системы Microsoft Excel. Программа Chemometrics Add-In предназначена для анализа данных методами Principal Component Analysis (PCA), Projection on Latent Structures (PLS1 и PLS2). Все вычисления производятся внутри рабочих книг Excel с помощью функций листа (worksheet functions) аналогично стандартным функциям, таким, как, например, МУМНОЖ. Предполагается, что читатель имеет базовые навыки работы в среде Excel, умеет проводить простейшие матричные вычисления с использованием функций листа. В пособии интенсивно используются понятия и методы матричной алгебры – вектор, матрица, и т.п. Читателям, которые плохо знакомы с этим аппаратом, рекомендуется изучить, или, хотя бы просмотреть, пособие "Матрицы и векторы". Настоящее пособие не является учебником по проекционным методам анализа многомерных данных. В нем приведены только основные формулы, поскольку они необходимы для понимания реализованных методов. Читатели, которые плохо знакомы с этим подходом, могут обратиться к Литературе. Изложение иллюстрируется примерами, выполненными в рабочей книге Excel Projection.xls, которая сопровождает этот документ. Важная информация о работе с файлом Projection.xls Ссылки на примеры помещены в текст как объекты Excel. По форме эти примеры имеют абстрактный, модельный характер, однако, по своей сути, они тесно связаны с задачами, встречающимися на практике 1. Проекционные методы1.1. Постановка задачиПроекционные методы интенсивно используются для анализа многомерных данных, прежде всего, в хемометрике. Они применяются и для одноблочных массивов X (классификация – PCA), так и для данных, состоящих из двух блоков X и Y (калибровка – PCR, PLS). Пусть имеется матрица переменных X размерностью (I×J), где I – число образцов (строк), а J – это число независимых переменных (столбцов), которых, как правило, много (J>>1). С другой стороны, может еще иметься матрица откликов Y, размерностью (I×K), где I – это, естественно, тоже число образцов, а K – это число откликов. Суть проекционного подхода состоит в существенном понижении размерности исходных массивов, как блока X, так и блока Y. Подробное описание проекционных методов можно найти в Литературе. 1.2. PCAСтарейшим проекционным методом является метод главных компонент (Principal Component Analysis – PCA). В этом методе используются новые, формальные переменные ta, (a=1,…A), являющиеся линейной комбинацией исходных переменных xj (j=1,…J) – ta=pa1x1+… paJxJ или в матричном виде – В этом уравнении T называется матрицей счетов (scores). Ее размерность – (I×A). Матрица P называется матрицей нагрузок (loadings). Ее размерность (A×J). E – это матрица остатков, размерностью (I×J).
Рис. 2 Графическое представление метода главных компонент Новые переменные ta называются главными компонентами (Principal Components), поэтому и сам метод называется методом главных компонент (PCA). Число столбцов – ta в матрице T, и pa в матрице P – равно A, которое называется числом главных компонент (PC). Эта величина заведомо меньше числа переменных J и числа образцов I. Имеют место следующие соотношения – TtT = Λ= diag{ λ1,…,λA}, PtP = I Для построения PCA счетов и нагрузок, используется рекуррентный алгоритм NIPALS, который на каждом шагу вычисляет одну компоненту. Сначала исходная матрица X преобразуется (как минимум – центрируется; см. раздел 1.4) и превращается в матрицу E0, a=0. Далее применяют следующий алгоритм.
После вычисления очередной (a-ой) компоненты, полагаем ta=t и pa=p. Для получения следующей компоненты надо вычислить остатки Ea+1 = Ea – t pt и применить к ним тот же алгоритм, заменив индекс a на a+1. Программа для реализации PCA в среде MatLab приведена в пособии MatLab. Руководство для начинающих. После того, как построено пространство из главных компонент, новые образцы Xnew могут быть на него спроецированы, иными словами – определены матрицы их счетов Tnew. В методе PCA это делается очень просто – Tnew.= Xnew P Разумеется, матрица Xnew новых образцов должен предварительно быть модифицирован так же, как и вектора из обучающего набора X, по которым строилось PCA подпространство 1.3. PLSОбобщением метода PCA является метод
проекций на латентные структуры (Projection
on Latent Structures, PLS), в котором проводится
одновременная декомпозиция матриц X
и Y Проекция строится согласованно – так, чтобы максимизировать корреляцию между соответствующими векторами X-счетов ta и Y-счетов ua.
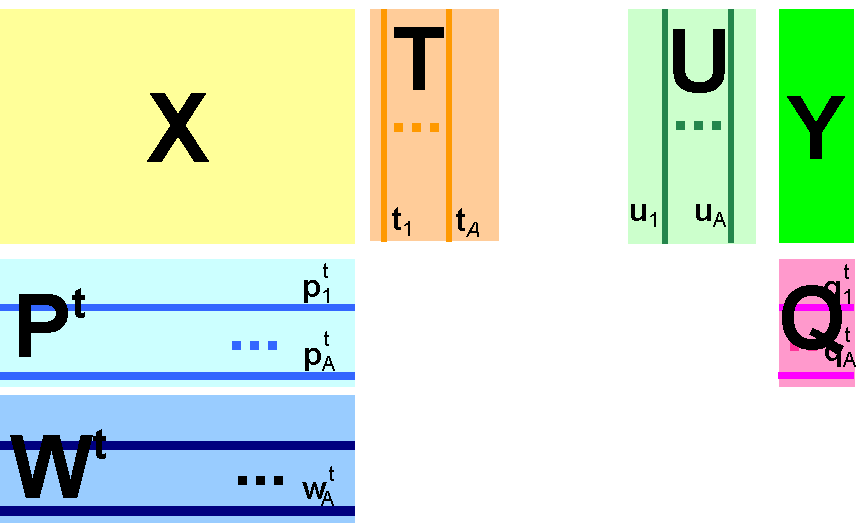
Рис. 3 Графическое представление метода главных компонент Если блок данных Y включает несколько откликов (т.е. K>1), можно построить две проекции исходных данных – PLS1 и PLS2. В первом случае для каждого из откликов yk строится свое проекционное подпространство. При этом и счета T (U) и нагрузки P (W, Q) , зависят от того, какой отклик используется. Этот подход называется PLS1. Для метода PLS2 строится только одно проекционное пространство, которое является общим для всех откликов. Имеют место следующие соотношения – TtT = Λ= diag{ λ1,…,λA}, WtW = I, T = XR, R = W(PtW)–1 RtP = I, Yhat = XB=TQt, B = RQt, Qt = Λ–1TtY, Wt = Λ–1UtX Для построения PLS счетов и нагрузок, используется рекуррентный алгоритм, который на каждом шагу вычисляет одну PLS компоненту. Для PLS1 алгоритм выглядит следующим образом. Исходная матрица X и вектор y преобразуют (как минимум – центрируют; см. раздел 1.4), и они превращаются в матрицу E0 и вектор f0, a=0. Далее к ним применяет следующий алгоритм.
После вычисления очередной (a-ой) PLS1 компоненты надо положить: ta=t, pa=p, wa=w, ua=u и qa=q. Для получения следующей компоненты надо вычислить остатки Ea+1 = Ea – t pt и fa+1 = fa – qt и применить к ним тот же алгоритм, заменив индекс a на a+1. Для PLS2 алгоритм выглядит следующим образом. Сначала исходные матрицы X и Y преобразуют (как минимум – центрируют; см. раздел 1.4), и они превращаются в матрицы E0 и F0, a=0. Далее к ним применяет следующий алгоритм.
После вычисления очередной (a-ой) PLS2 компоненты надо положить: ta=t, pa=p, wa=w, ua=u и qa=q. Для получения следующей компоненты надо вычислить остатки Ea+1 = Ea – t pt и Fa+1 = Fa – tqt и применить к ним тот же алгоритм, заменив индекс a на a+1. Программы для реализации PLS1 и PLS2 в среде MatLab приведены в MatLab. Руководство для начинающих Вычисление счетов Tnew и Unew для новых образцов (Xnew , Ynew) в методе PLS сложнее, чем в PCA. Для PLS1, матрица Xnew , и вектор ynew модифицируются так же, как и в обучающем наборе и превращаются в E0 и f0, a=0. Далее к ним применяет следующий алгоритм для вычисления счетов для a=1,…, A компонент
После вычисления очередной (a-ой) PLS1 компоненты надо вычислить новые остатки Ea+1 = Ea – t pt и fa+1 = fa – qt и применить к ним тот же алгоритм, заменив индекс a на a+1. В методе PLS2 новые матрицы Xnew и Ynew модифицируются так же, как и в обучающем наборе, и они превращаются в матрицы E0 и F0, a=0. Далее к ним применяет следующий алгоритм для a=1,…, A компонент
После вычисления a-ой PLS2 компоненты надо вычислить новые остатки Ea+1 = Ea – tpt и Fa+1 = Fa – tqt и применить к ним тот же алгоритм, заменив индекс a на a+1 1.4. Подготовка данныхСледует обратить внимание на то, что, и PCA, и PLS методы не учитывают свободного члена при разложении матриц X и Y. Это видно из формул (1) и (2). В них исходно предполагается, что все столбцы матриц X и Y имеют нулевое среднее, т.е.,
Это условие легко можно удовлетворить, проведя центрирование данных. Центрирование – это вычитание из исходной матрицы X матрицы M, т.е. Обычно усреднение проводится по столбцам: для каждого вектора xj вычисляется среднее значение –
Тогда M=(m11,..., mJ1), где 1 – это вектор из единиц размерности I. Центрирование – это почти обязательная процедура перед применением проекционных методов. Второе простейшее преобразование данных, нормирование, не является столь обязательным. Нормирование, в отличие от центрирования, не меняет структуру данных, а просто изменяет вес различных частей данных при обработке. Чаще всего применяется нормирование по столбцам – это умножение исходной матрицы X справа на матрицу W, т.е. .
Матрица W – это диагональная матрица размерности J×J. Обычно диагональные элементы wjj равны обратным значениям стандартного отклонения.
вычисленным для каждого столбца xj. Нормирование по строкам (называемое также нормализацией) – это умножение матрицы X слева на диагональную матрицу W, т.е.
При этом размерность W равна I×I, а ее элементы wii – это обратные значения стандартных отклонений строк xit Комбинация центрирования и нормирования по столбцам
называется автошкалированием. Нормирование данных часто применяют для того, чтобы уравнять вклад в модель от различных переменных (например, в гибридном методе ЖХ-МС), учесть неравномерные погрешности, или для того, чтобы обрабатывать совместно разные блоки данных. Нормирование также можно рассматривать как метод, позволяющий стабилизировать вычислительные алгоритмы. В тоже время, к этому преобразованию нужно относиться с большой осторожностью, т.к. оно может сильно исказить результаты качественного анализа. Любое преобразование данных – центрирование, шкалирование, и т.п. – всегда делается сначала на обучающем наборе. По этому набору находятся значения mj и dj, которые затем применяются и к обучающему, и к проверочному набору 1.5. ПрограммыПроекционные методы реализованы в нескольких популярных программах, краткий обзор которых приведен в этом разделе. Чаще всего используются специализированные пакеты. Среди них – программа SIMCA, разработанная компанией Umetrics, и аналогичный пакет Unscrambler, компании Camo. В тройку самых популярных пакетов входит также PLS ToolBox компании Eigenvector Research, Inc. Первые две программы функционируют независимо (stand alone), тогда как последняя работает только внутри вычислительной среды MatLab. Многие проекционные методы реализованы в статистических пакетах общего назначения, таких как Statistica, SPSS и в ряде других. Существует одна условно свободно распространяемая программа. Это – Multivariate Analysis Add-in – надстройка для Excel, разработанная в Хемометрическом центре Бристольского университета под руководством проф. Р. Бреретона 1.6. Модельный примерДля иллюстрации работы надстройки Chemometrics Add-In используется модельный пример, помещенный в файл Projection.xls. В нем приведены данные (X, Y), к которым применяются описанные здесь процедуры. Данные нуждаются в центрировании, но не требуют шкалирования. Файл Projection.xls. включает в себя следующие листы:
2. Использование надстройки Chemometrics Add-In2.1. УстановкаПрежде чем использовать надстройку Chemometrics Add-In, необходимо ее установить. В состав установочного пакета входят два файла Chemometrics.dll и Chemometrics.xla. Установочный пакет с демонстрационной версией надстройки Chemometrics Add-In можно скачать здесь. Демонстрационная версия ничем не отличается от полной, однако она работает только с "нашими" файлами: Calibration.xls, Excel.xls, Projections.xls, и т.д. Эти файлы можно изменять, но сохранять эти изменения нельзя. Полная версия может быть предоставлена по запросу. Инструкция по установки надстройки Chemometrics Add-In находится здесь. 2.2. Общие сведенияНадстройка Chemometrics Add-In получает всю исходную информацию из открытой рабочей книги Excel. Эта информация должна быть помещена в массивах непосредственно на рабочий лист (данные X и Y). Пользователь может организовать рабочее пространство так, как ему удобно – использовать только один лист для размещения всей информации, или несколько листов, или даже листы в разных рабочих книгах. Полученные результаты также выводятся как массивы на листах рабочей книги. Программа не имеет ограничений на размер входной информации – количество образцов (I), переменных (J), и откликов (K) в данных. Размер данных ограничен только объемом памяти, который поддерживает операционная система, установленная на компьютере, а также ограничениями, налагаемыми программой Excel. Надстройка Chemometrics Add-In содержит
несколько функций, которыми можно
пользоваться как обычными функциями
рабочего листа Excel. Для этого надо
активизировать Мастер
функций Результатами работы этих функций являются массивы, поэтому они должны быть введены как формулы массива, т.е. с применением комбинации клавиш . Аргументы функций должны быть числами или именами, массивами или ссылками, содержащими числа. При вводе формулы необходимо обводить на листе массив, размеры которого соответствуют объему получаемой информации. При задании большего, чем следует массива, в излишних клетках выводятся символы #N/A. В противном случае, т.е. когда размеры массива вывода меньше, чем следует, часть результатов, лежащих за пределами массива, не выводится на лист. Число
главных компонент Центрирование
и/или шкалирование
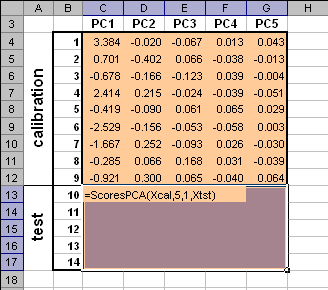
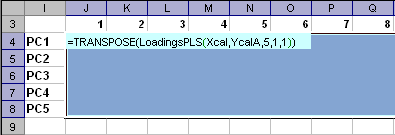
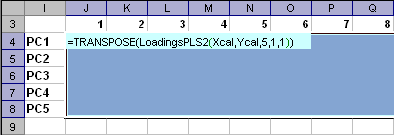
Если аргумент CentWeightX или CentWeightY опущен, то предполагается, что он равен 0. 3. PCA3.1. ScoresPCAВозвращает значения счетов T в соответствии с уравнением (1) метода главных компонент по заданным значениям матрицы X и Xnew. Синтаксис ScoresPCA (X [, PC] [,CentWeightX] [, Xnew])
Примечания
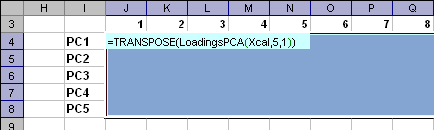
Пример Рис. 4 Пример ввода функции ScoresPCA Функция ScoresPCA является формулой массива и ее ввод должен завершаться нажатием комбинации . 3.2. LoadingsPCAВозвращает значения нагрузок P в соответствии с уравнением (1) метода главных компонент по заданным значениям матрицы X. Синтаксис LoadingsPCA (X [, PC] [, CentWeightX])
Примечания
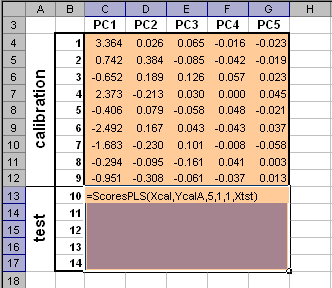
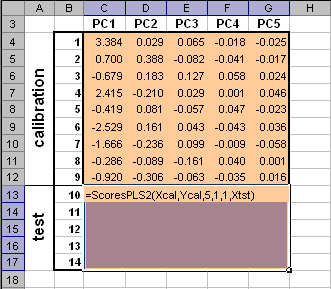
Пример Рис. 5 Пример ввода функции LoadingsPCA Функция LoadingsPCA является формулой массива и ее ввод должен завершаться нажатием комбинации . 4. PLS4.1. ScoresPLSВозвращает значения PLS счетов T в соответствии с уравнением (2) метода PLS по заданным значениям матриц X и Y , а также матрицы Xnew . Синтаксис ScoresPLS (X, Y [, PC] [, CentWeightX] [, CentWeightY] [, Xnew] )
Примечания
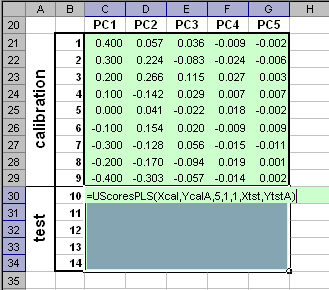
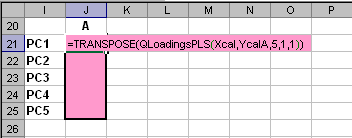
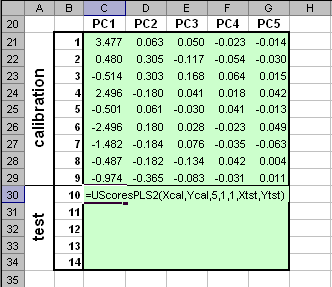
Пример Рис.6 Пример ввода функции ScoresPLS Функция ScoresPLS является формулой массива и ее ввод должен завершаться нажатием комбинации . 4.2. UScoresPLSВозвращает значения счетов U в соответствии с уравнением (2) метода PLS по заданным значениям матриц X и Y , а также матриц Xnew и Ynew. Синтаксис UScoresPLS (X, Y, [, PC] [, CentWeightX] [, CentWeightY] [, Xnew][, Ynew])
Примечания
Пример Рис.7 Пример ввода функции UScoresPLS Функция UScoresPLS является формулой массива и ее ввод должен завершаться нажатием комбинации . 4.3 LoadingsPLSВозвращает значения нагрузок P в соответствии с уравнением (2) метода PLS по заданным значениям матриц X и Y. Синтаксис LoadingsPLS (X, Y [, PC] [, CentWeightX] [, CentWeightY])
Примечания
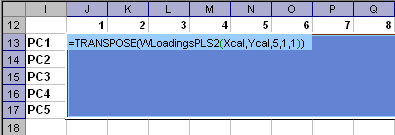
Пример Рис. 8 Пример ввода функции LoadingsPLS Функция LoadingsPLS является формулой массива и ее ввод должен завершаться нажатием комбинации . 4.4 WLoadingsPLSВозвращает значения нагрузок W в соответствии с уравнением (2) метода PLS по заданным значениям матриц X и Y. Синтаксис WLoadingsPLS (X, Y [, PC] [, CentWeightX] [, CentWeightY])
Примечания
Пример Рис. 9 Пример ввода функции WLoadingsPLS Функция WLoadingsPLS является формулой массива и ее ввод должен завершаться нажатием комбинации . 4.5 QLoadingsPLSВозвращает значения нагрузок Q в соответствии с уравнением (2) метода PLS по заданным значениям матриц X и Y. Синтаксис QLoadingsPLS (X, Y [, PC] [, CentWeightX] [, CentWeightY])
Примечания
Пример Рис. 10 Пример ввода функции QLoadingsPLS Функция QLoadingsPLS является формулой массива и ее ввод должен завершаться нажатием комбинации . 5. PLS25.1. ScoresPLS2Возвращает значения PLS2 счетов T в соответствии с уравнением (2) метода PLS2 по заданным значениям матриц X и Y , а также матрицы Xnew. Синтаксис ScoresPLS2(X, Y [, PC] [, CentWeightX] [, CentWeightY] [, Xnew] )
Примечания
Пример Рис.11 Пример ввода функции ScoresPLS2 Функция ScoresPLS2 является формулой массива и ее ввод должен завершаться нажатием комбинации . 5.2. UScoresPLS2Возвращает значения счетов U в соответствии с уравнением (2) метода PLS2 по заданным значениям матриц X и Y , а также матриц Xnew и Ynew. UScoresPLS2 (X, Y, [, PC] [, CentWeightX] [, CentWeightY] [, Xnew][, Ynew]) Синтаксис
Примечания
Рис.12 Пример ввода функции UScoresPLS2 Функция UScoresPLS2 является формулой массива и ее ввод должен завершаться нажатием комбинации . 5.3 LoadingsPLS2Возвращает значения нагрузок P в соответствии с уравнением (2) метода PLS2 по заданным значениям матриц X и Y. Синтаксис LoadingsPLS2 (X, Y [, PC] [, CentWeightX] [, CentWeightY])
Примечания
Пример Рис. 13 Пример ввода функции LoadingsPLS2 Функция LoadingsPLS2 является формулой массива и ее ввод должен завершаться нажатием комбинации . 5.4 WLoadingsPLS2Возвращает значения нагрузок W в соответствии с уравнением (2) метода PLS2 по заданным значениям матриц X и Y. Синтаксис WLoadingsPLS2 (X, Y [, PC] [, CentWeightX] [, CentWeightY])
Примечания
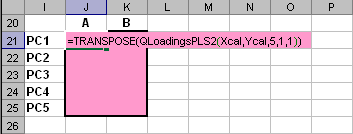
Пример Рис. 14 Пример ввода функции WLoadingsPLS2 Функция WLoadingsPLS2 является формулой массива и ее ввод должен завершаться нажатием комбинации . 5.5 QLoadingsPLS2Возвращает значения нагрузок Q в соответствии с уравнением (2) метода PLS2 по заданным значениям матриц X и Y. Синтаксис QLoadingsPLS2 (X, Y [, PC] [, CentWeightX] [, CentWeightY])
Примечания
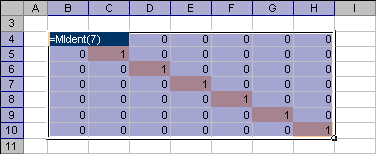
Пример Рис. 15 Пример ввода функции QLoadingsPLS2 Функция QLoadingsPLS2 является формулой массива и ее ввод должен завершаться нажатием комбинации . 6. Дополнительные матричные функции6.1. MIdentВозвращает единичную квадратную матрицу Синтаксис MIdent(Size)
Примечание
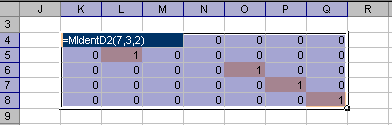
Пример Рис. 16 Пример ввода/вывода функции MIdent Функция MIdent является формулой массива и ее ввод должен завершаться нажатием комбинации . 6.2. MIdentD2Возвращает матрицу из нулей и единиц, получившуюся в результате вырезание блока строк из единичной матрицы Синтаксис MIdentD2(Size, CutFrom, CutOff)
Примечание
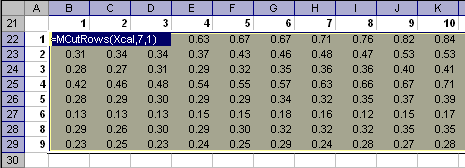
Пример Рис. 17 Пример ввода/вывода функции MIdentD2 Функция MIdentD2 является формулой массива и ее ввод должен завершаться нажатием комбинации . 6.3. MCutRowsВозвращает матрицу у которой вырезан блок строк Синтаксис MCutRows(X, CutFrom, CutOff)
Примечание
Пример Рис. 18 Пример ввода/вывода функции MCutRows Функция MCutRows является формулой массива и ее ввод должен завершаться нажатием комбинации . Содержание
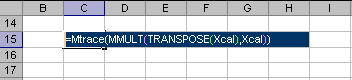
Возвращает след матрицы MTrace(X)
Примечание
Пример Рис. 18 Пример ввода/вывода функции MTrace Функция MTrace не является формулой массива и ее ввод может завершаться нажатием одной клавиши ЗаключениеНадстройка Chemometrics Add-In дает возможность вычисления разных величин (счетов, нагрузок), связанных с проекционным представлением исходных данных. Далее, комбинируя эти показатели, можно создать типичные графики, применяемые в анализе данных (например, графики счетов и нагрузок), построить калибровки, найти такие важные характеристики как среднеквадратичные остатки калибровки (RMSEC) и при проверке (RMSEP), и т.п. Примеры приведены в пособиях:
|

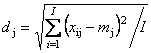
 (
(