Статистика
СодержаниеВведениеВ этом документе собраны основные сведения из математической статистики, которые используются в хемометрике. Приведенный текст не может служить учебником по статистике – это скорее конспект, краткий справочник по математической статистике. Более глубокое и систематическое изложение может быть найдено в литературе. Изложение иллюстрируется примерами, выполненными в рабочей книге Excel Statistics.xls, которая сопровождает этот документ. Важная информация о работе с файлом Statistics.xls Ссылки на примеры помещены в текст как объекты Excel.1. Базовые сведения1.1. Вероятность событияВ мире часто происходят события, исход которых не предопределен заранее. Всем известен хрестоматийный пример с подбрасыванием монетки, завершающийся случайным событием: выпадением орла или решки. Таким случайным событиям можно приписать вероятность – число от нуля до единицы. Однако не у всякого события может быть вероятность. Ключевым условием является повторяемость. Поэтому бессмысленно спрашивать, какова вероятность того, что завтра пойдет дождь. У «завтра» нет повторяемости – это уникальное событие, которое нельзя повторить. Однако можно говорить о вероятности того, что 7 июля будет дождь. Событие «7 июля» повторяется каждый год, и дождю в этот день можно приписать некоторую вероятность. Понятие вероятности можно применять только к тем событиям, которые еще не произошли, или исход которых нам пока не известен. Так, например, мы можем рассчитать вероятность выигрыша в лотерею, но, как только нам стал известен результат розыгрыша, т.е. событие уже произошло – рассчитанная вероятность теряет всякий смысл. Еще одним важным понятием является пространство событий – это полный набор всех возможных исходов. Так в опыте с монеткой есть только два события: орел и решка. Рассмотрим другой опыт – измерение роста случайно выбранного человека. Если точность измерения один сантиметр, то пространство событий – это набор чисел от 30 см (новорожденный), до 251 см (рекорд книги Гиннеса) – всего 222 варианта. Однако если мы меряем рост с точность до 1 метра, то в пространстве оказываются только три события: меньше 1 м, от 1 м до 2 м, и больше 2 м. 1.2. Случайная величинаСлучайная величина — это переменная, значение которой до опыта (реализации) неизвестно. Всякая случайная величина характеризуется:
Множество значений может быть дискретным, непрерывным и дискретно-непрерывным. Соответственно именуются и случайные величины. 1.3. Распределение случайной величиныПусть X – это случайная величина, множеством возможных значений которой являются действительные числа. Рассмотрим вероятность события, что реализация X не больше заданного числа x. Если рассматривать эту вероятность в зависимости от величины x, то получится функция F(x), называемая (кумулятивной) функцией распределения случайной величины –
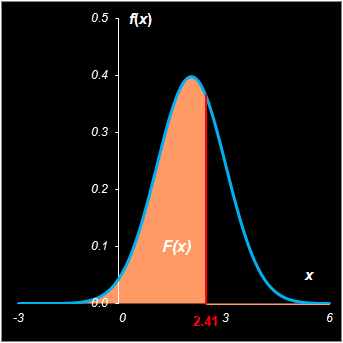
Функция распределения это неубывающая функция, которая стремится к 0 при малых x, и стремится к 1 при больших значениях аргумента. То, что случайная величина X имеет функцию распределения F обозначается так – X ~ F. Распределение называется симметричным (относительно точки a) если F(a+x)=1–F(a–x). Для дискретных случайная величина функция распределения кусочно-постоянна со скачками в точках x=xi. Производная функция распределения F(x) называется плотностью вероятности f(x)
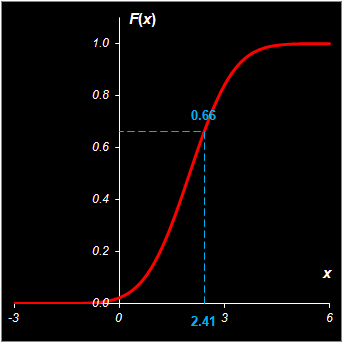
Рис. 1 плотность вероятности f(x) и ф.р F(x) случайной величины 1.4. Математическое ожиданиеПусть X – это случайная величина с плотностью вероятности f(x). Математическим ожиданием X называется величина
1.5. Дисперсия и СKОПусть X – это случайная величина с плотностью вероятности f(x). Дисперсией X называется величина
Если из дисперсии извлечь квадратный корень, то получится величина, называемая среднеквадратичным отклонением (СКО). 1.6. МоментыПусть X – это случайная величина с плотностью вероятности f(x). Моментом порядка n называется величина
По определению μ1 = E(X). Центральным моментом порядка n называется величина
По определению m2= V(X). 1.7. КвантилиПусть F(x) – (кумулятивная) функция распределения случайной величины
Рассмотрим функцию F–1(P), 0≤P≤1, обратную к F(x) т.е. F–1(F(x))=x F(F–1(P))=P . Функция F–1(P) называется P-квантилем распределения F. Величина квантиля для P=0.5 называется медианой распределения. Квантили для P=0.25, 0.75 называются квартилями, а для P=0.01, 0.02, …, 0.99 называются процентилями. 1.8. Многомерные распределенияДве (и более) случайные величины можно рассматривать совместно. Совместная (кумулятивная) функция распределения двух случайных величин X и Y определяется так
Так же, как и в одномерном случае, функция f(x, y) называется плотностью вероятности . Случайные величины X и Y называются независимыми, если их совместная плотность вероятности равна произведению частных плотностей.
1.9. Ковариации и корреляцииКовариацией случайных величин X и Y называется (детерминированная) величина
где f(x, y) – совместная плотность вероятности . Величина
называется корреляцией случайных величин X и Y. Если случайные величины X и Y независимы, то их ковариация и корреляция равны нулю. Обратное не верно. Для совместных распределений многомерных случайных величин X1,…, Xn ковариационная матрица C cij=cov(Xi, Xj), i, j=1,…, n играет ту же роль, что и дисперсия в одномерном распределении. 1.10. Функции от случайной величиныФункция от случайной величины также является случайной величиной. Пусть случайная величина X имеет функцию распределения FX(x), и случайные величины X и Y связаны взаимно однозначными соотношениями y=φ(x) x=ψ(y) . Если φ(x) – возрастающая функция, то функция распределения и квантили случайной величины Y определяются так FY(y) = FX(ψ(y)) y(P)= φ(x(P)) . Если ψ(y) – дифференцируемая функция, то плотность вероятности случайной величины Y вычисляется по формуле
Для линейных преобразований y=ax+b
1.11. Стандартизация случайной величиныЕсли случайная величина X имеет математическое ожидание m и дисперсию s2: E(X)=m, V(X)=s2, то случайная величина Y=(X–m)/s называется стандартизованной (нормированной), поскольку E(Y)=0 V(Y)=1. 2. Основные распределения2.1. Биномиальное распределениеДискретная случайная величина X имеет дискретное биномиальное распределение, если ее плотность вероятности имеет вид
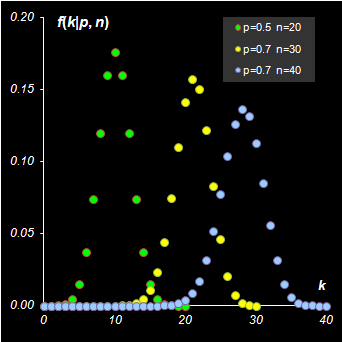
где Биномиальное распределение – это распределение числа успехов k в серии из независимых n опытов, при условии, что вероятность успеха в каждом опыте есть p. Математическое ожидание и дисперсия, соответственно, равны
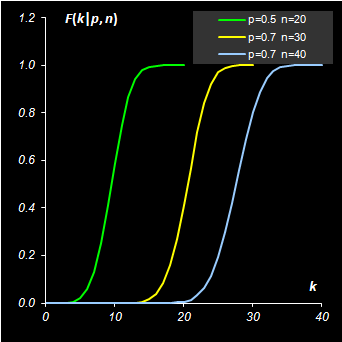
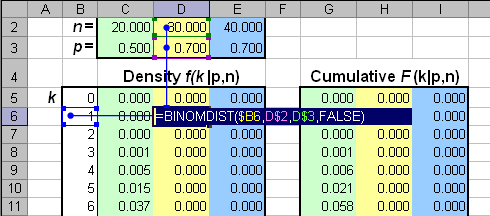
При больших n биномиальное распределение хорошо приближается нормальным с параметрами (5) . Рис. 2 плотность вероятности и функция распределения биномиального распределения Для вычисления биномиального распределения в Excel используется стандартная функция BINOMDIST (БИНОМРАСП). Синтаксис BINOMDIST(number_s=k, trials=n, probability_s=p ,cumulative=TRUE|FALSE)
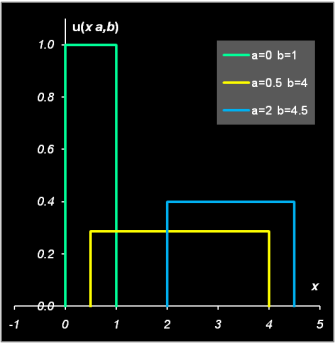
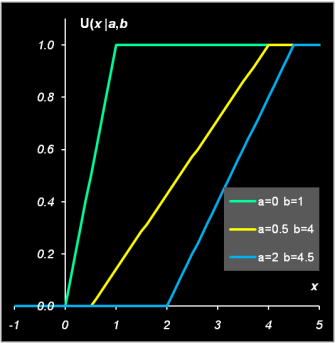
Рис. 3 Пример вычисления биномиального распределения 2.2. Равномерное распределениеСлучайная величина X распределена равномерно на отрезке [a, b], если ее функция распределения U(x|a,b) и, соответственно, плотность вероятности u(x|a,b) имеют вид
Математическое ожидание и дисперсия, соответственно, равны E(X)=0.5(a+b), V(X)=(b−a)2/12 .
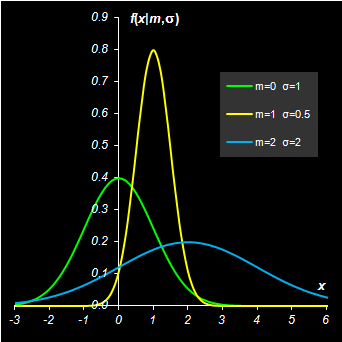
Рис. 4 Плотность вероятности и функция распределения равномерного распределения То, что случайная величина X распределена равномерно на отрезке[a, b], будем обозначать X ~ U(a, b). 2.3. Нормальное распределениеНормальное (или гауссово) распределение – это, наверное, самое важное распределение в статистике. Плотность этого распределения имеет вид
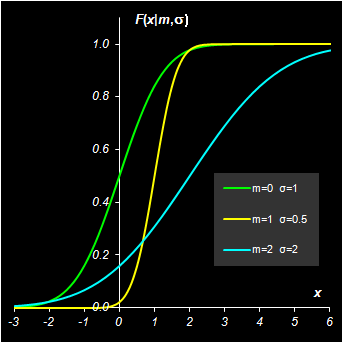
Нормальное распределение зависит от двух параметров: m и σ2 и оно обычно обозначается N(m, σ2) т.е. X ~ N(m, σ2). Математическое ожидание и дисперсия нормального распределения равны, соответственно E(X)=m, V(X)=σ2. Нормальное распределение называется стандартным, если m=0, σ2=1. Если X0 ~ N(0, 1), то X= m+ σX0 ~ N(m, σ2). Кумулятивная функция стандартного нормального распределения
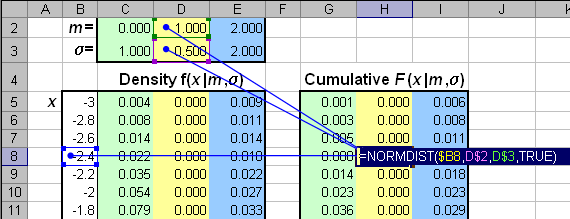
является специальной функцией, т.к. она не выражается через элементарные функции. Квантили стандартного нормального распределения обозначаются Φ–1(P). Стандартное нормальное распределение симметрично, поэтому для него верны следующие соотношения Φ(–x)=1– Φ(x) Φ–1(1–P) = – Φ–1(P) Рис. 5 Функция распределения и плотность вероятности нормального распределения Для вычисления нормального распределения в Excel используется стандартные функции: NORMDIST (НОРМРАСП) и NORMSDIST (НОРМСТРАСП), а также NORMINV (НОРМОБР) и NORMSINV (НОРМСТОБР). Синтаксис NORMDIST(x, mean=m, standard_dev= σ, cumulative=TRUE|FALSE) Если cumulative=TRUE то возвращается кумулятивная функция распределения Φ(x|m, σ2), а если cumulative=FALSE , то возвращается плотность вероятности (6). NORMSDIST(x) Возвращается кумулятивная функция стандартного нормального распределения в точке x. NORMINV(probability=P, mean=m, standard_dev= σ) Возвращается квантиль Φ–1(P|m, σ2) нормального распределения для вероятности P. NORMSINV(probability =P) Возвращается квантиль Φ–1(P|0, 1) стандартного нормального распределения для вероятности P. Рис.6 Пример вычисления нормального распределения 2.4. Распределение хи-квадратРассмотрим N независимых стандартных нормальных случайных величин X1,…, Xn,…, XN с нулевым мат. ожиданием и единичной дисперсией, т.е. Xn ~ N(0, 1). Величина
является случайной, распределение которой носит название хи-квадрат. Это распределение зависит от одного параметра – N, который называется числом степеней свободы. Плотность вероятности распределения хи-квадрат имеет вид
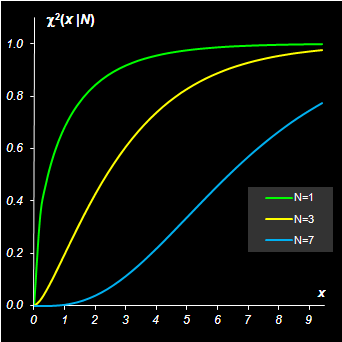
Распределение хи-квадрат широко используется в статистике, например, при проверке гипотез. Математическое ожидание и дисперсия распределения χ2(N) равны, соответственно,
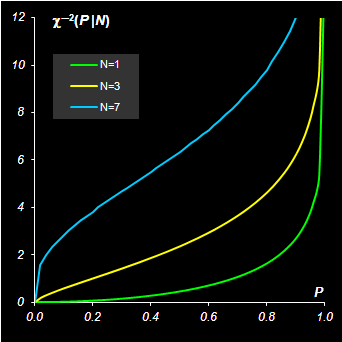
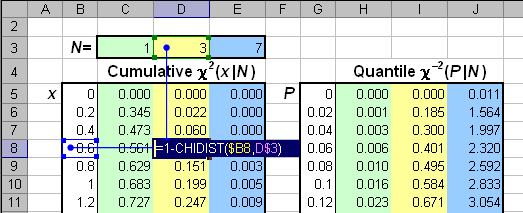
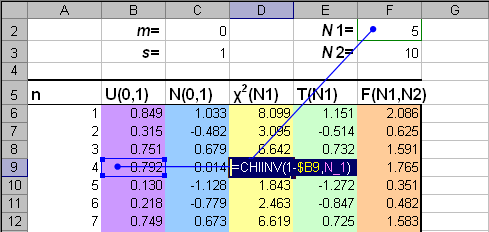
При больших N распределение хи-квадрат хорошо приближается нормальным с параметрами (7). Квантили распределения χ2(N) обозначаются χ–2(P|N). Рис.7 функция распределения и квантиль распределения хи-квадрат Для вычисления распределения хи-квадрат в Excel используется две стандартные функции: CHIDIST (ХИ2РАСП) и CHIINV (ХИ2ОБР). Синтаксис CHIDIST(x, degrees_freedom=N) Возвращается значение 1 – χ2(x|N), где χ2(x|N) – кумулятивная функция распределения хи-квадрат. CHIINV(probability=1–P ,degrees_freedom=N) Возвращается квантиль χ–2(1 – P|N) распределения хи-квадрат для вероятности 1 – P. Рис.8 Пример вычисления распределения хи-квадрат
2.5. Распределение СтьюдентаРассмотрим две случайные величины: X – распределенную стандартно-нормально X ~ N(0, 1), и Y – распределенную по хи-квадрат с N степенями свободы Y ~ χ2(N). Случайная величина
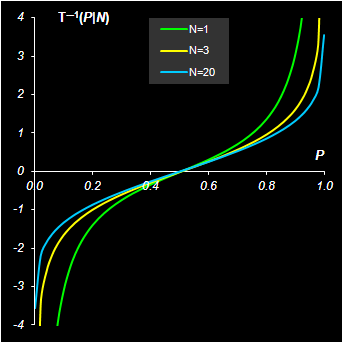
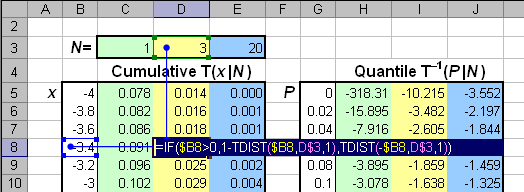
подчиняется распределению, которое носит имя Стьюдента. Это распределение зависит от одного параметра N, который также называется числом степеней свободы. Распределение Стьюдента применяется в проверке гипотез и для построения доверительных интервалов. Математическое ожидание T(N) равно нулю, а дисперсия равна V(T(N))=N/(N–2), N>2. Распределение Стьюдента симметрично, и при N>20 неотличимо от нормального. Формула для плотности вероятности Стьюдента приведена во многих пособиях. Квантили распределения T(N) обозначаются T–1(P|N). Рис.9 Функция распределения и квантиль распределения Стьюдента Для вычисления распределения Стьюдента в Excel используется две стандартные функции: TDIST (СТЬЮДРАСП) и TINV (СТЬЮДРАСПОБР). Синтаксис TDIST(x, degrees_freedom=N, tails=1|2) Если tails = 1, то функция TDIST возвращает значение Pr{T(N) > x }, а при tails = 2 значение Pr{|T(N)| > x}. Значения при x<0 не возвращаются. Поэтому, для того, чтобы вычислить в Excel обычную кумулятивную функцию распределения Стьюдента T(x|N), приходится использовать следующую формулу IF(x>0, 1-TDIST(x,N,1), -TDIST(-x,N,1)) . TINV(probability, degrees_freedom=N) Возвращается значение x, для которого Pr{|T(N)| > x } = probability. И в этом случае для вычисления в Excel квантиля распределения Стьюдента T–1(P|N), нужно использовать следующую формулу IF(P<0.5, TINV(2*P,N), -TINV(2-2*P,N)). Рис.10 Пример вычисления распределения Стьюдента 2.6. Распределение ФишераПусть имеются две независимые случайные величины X1 и X2 , каждая из которых подчиняется распределению хи-квадрат с N1 и N2 степенями свободы, т.е. X1 ~ χ2(N1) и X2 ~ χ2(N2). Случайная величина
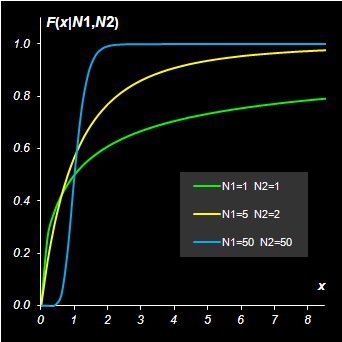
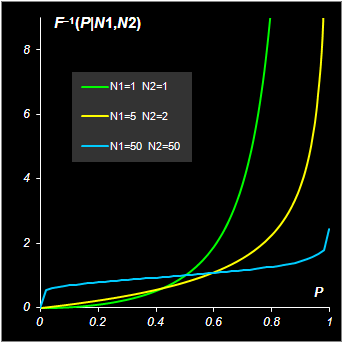
подчиняется распределению, которое носит имя Фишера. Это распределение зависит от двух параметров N1 и N2, которые также называются числами степеней свободы. Математическое ожидание и дисперсия распределения F(N1, N2) равны , соответственно, E(F(N1, N2))= N2/(N2 –2), N2>2
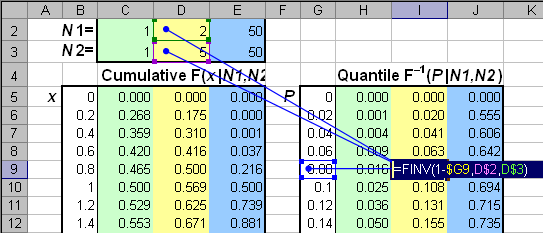
Формула для плотности вероятности распределения Фишера приведена во многих пособиях. Если X~ F(N1, N2), то 1/X~ F(N2, N1). Квантили распределения F(N1, N2) обозначаются F–1(P|N1, N2). Рис.11 Функция распределения и квантиль распределения Фишера Для вычисления распределения Фишера в Excel используются две стандартные функции: FDIST (FРАСП) и FINV (FРАСПОБР). Синтаксис FDIST(x, degrees_freedom1= N1, degrees_freedom2= N2) Возвращается значение 1 – F(x|N1, N2), где F(x|N1, N2) – кумулятивная функция распределения Фишера. FINV(probability=1–P, degrees_freedom1= N1, degrees_freedom2= N2) Возвращается квантиль F–1(1 – P|N1, N2) для вероятности 1 – P. Рис.12 Пример вычисления распределения Фишера 2.7. Многомерное нормальное распределениеЭто распределение является естественным обобщением одномерного нормального распределения на случай многомерной случайной величины, т.е. случайного вектора x, размерностью n. Функция плотности вероятности имеет следующий вид
где Σ – симметричная положительно определенная (n ×n) матрица. Многомерное нормальное распределение зависит от двух групп параметров: x ~ N(m, Σ). Математическое ожидание x равно m, а ковариационная матрица равна матрице Σ. 2.8. Генерация случайных чиселИногда бывает полезно создать искусственную выборку случайных чисел, подчиняющихся заданному распределению. Это можно сделать, используя следующее простое утверждение. Пусть F(x) и F–1(P) суть некоторая функция распределения и ее квантиль, соответственно. Если случайная величина X распределена равномерно на отрезке [0, 1], т.е X ~ U(0,1), тогда случайная величина Y = F–1(X) имеет функция распределения F. Таким образом, если получить набор случайных величин, распределенных равномерно, то эти случайные величины можно превратить в новые, имеющие другое, заданное распределение. Для генерации случайных чисел в Excel имеется стандартная функция: RAND (СЛЧИС) . Синтаксис RAND() Возвращает случайное число, равномерно распределенное на отрезке [0,1]. Новое случайное число возвращается при каждом вычислении рабочего листа. На листе Random приведен пример генерации случайных чисел для разных распределений. Рис.13 Пример генерации случайных чисел 3. Оценка параметров3.1. ВыборкаПредположим, что имеется набор чисел x=(x1,…, xI ), и каждое xi является одной реализацией случайной величины, подчиняющейся, вообще говоря, неизвестному распределению. Этот набор называется выборкой, а число I – объемом выборки. В случае одномерного распределения выборка – это вектор x, а в многомерном случае выборка – это матрица X размерностью I×J , каждая строка которой представляет одну реализацию (наблюдение) многомерной случайной величины размерностью J. Обычно предполагается, что все элементы выборки статистически независимы. В практических приложениях слово «выборка» часто заменяется словом «данные». 3.2. Выбросы и маргиналыСреди элементов выборки могут присутствовать такие, которые существенно отличаются от других элементов. Пусть, например, имеется выборка из стандартного нормального распределения N(0,1), в которой присутствует элемент со значением xout=3.2. Для такого распределения вероятность единичного события xout ≥ 3.2 мала – она равна α=0.0007. Однако значение xout присутствует в независимой выборке размера I, поэтому нужно рассчитывать вероятность события «хотя бы один раз среди I попыток»
Для I=10 Pout=0.007, для I=100 Pout=0.07, а для I=1000 Pout=0.50. Естественно – чем больше выборка, тем выше вероятность того, что встретится такое экстремальное значение. Таким образом, интерпретация выпадающих из выборки значений существенно зависит от объема выборки – для малых I их нужно рассматривать как выбросы (промахи при измерениях) и, соответственно, удалять из выборки. Для больших I такие выпадающие значения являются приемлемыми маргиналами и они должны сохраняться в выборке. 3.3. Генеральная совокупностьОперацию создания выборки в статистике называют извлечением. Тем самым подчеркивают, что имеющаяся у нас выборка x1 не единственная, и что можно получить (часто только теоретически) и другие похожие выборки x2 , x3, …., xn. Слово похожие означает, что все эти выборки устроены аналогичным способом – подчиняются одному и тому же распределению, имеют одинаковый объем I, и т.п. Все бесконечное множество таких выборок образуют генеральную совокупность (называемую также популяцией). 3.4. СтатистикаВ математике слово «статистика» имеет два значения. Во-первых, так называется раздел математики, в котором по выборке (результатам экспериментов) определяется вид распределения, из которого была извлечена эта выборка, оцениваются параметры этого распределения, проверяются гипотезы о виде этого распределения. Второе значение слова «статистика» – это (измеримая) функция выборки. Поскольку элементы выборки суть случайные величины, то и статистика является случайной величиной. Назначение статистик – оценка параметров распределения, из которого извлечена выборка. Примеры таких оценок приведены ниже. 3.5. Выборочное среднее и выборочная дисперсияВыборочным средним называется статистика Для вычисления выборочной дисперсии используются две статистики: - для случая выборки с неизвестным средним - и для известного среднего значения m Аналогичным образом определяются выборочные моменты, например, является оценкой k-ого центрального момента. Для вычисления выборочных статистик в Excel используют следующие стандартные функции :AVERAGE (СРЗНАЧ), VAR (ДИСП), VARP (ДИСПР), STDEV (СТАНДОТКЛОН), STDEVP (СТАНДОТКЛОНП). Синтаксис AVERAGE (x) Возвращает среднее значение выборки x, вычисленное по формуле (8). VAR (x) Возвращает выборочную дисперсию выборки x, вычисленную по формуле (9). VARP (x) Возвращает выборочную дисперсию выборки x, вычисленную по формуле (10). STDEV (x) Возвращает среднеквадратичное отклонение т.е. корень квадратный из выборочной дисперсии выборки x, вычисленной по формуле (9). STDEVP (x) Возвращает среднеквадратичное отклонение т.е. корень квадратный из выборочной дисперсии выборки x, вычисленной по формуле (10). 3.6. Выборочные ковариации и корреляцииЕсли имеются две выборки x=(x1,…, xI) и y=(y1,…, yI ), то можно рассчитать выборочные значения ковариации и корреляции. Ковариация c рассчитывается по формуле
а коэффициент корреляции r по формуле
В более общем случае, когда имеется матрица данных X, размерностью I наблюдений на J переменных, то выборочная матрица ковариаций CI между наблюдениями рассчитывается так – CI=XXt . Выборочная матрица ковариаций CJ между переменными так – CJ=XtX . Для вычисления парных ковариаций в Excel используют следующие стандартные функции: COVAR (КОВАР), CORREL (КОРРЕЛ). Синтаксис COVAR(x, y)Возвращает выборочную ковариацию между выборками x и y. CORREL(x, y)Возвращает выборочный коэффициент корреляции между выборками x и y. 3.7. Вариационный ряд и порядковые статистикиИсходную выборку (x1,…, xI) можно упорядочить в порядке неубывания : x(1) ≤ x(2) ≤ …≤ x(i) ≤… ≤ x(I) , и получить т.н. вариационный ряд. Элементы этого ряда являются порядковыми статистиками. Центральный элемент ряда (а если I – четное, то полусумма двух центральных) является выборочной оценкой медианы Аналогичным способом строятся оценки квартилей и процентилей. Размахом выборки называется величина x(I) – x(1) . Интерквартильным размахом выборки x называется величина
являющаяся разностью выборочных квартилей для P=0.75 и P=0.25. Для вычисления порядковых статистик в Excel используют следующие стандартные функции: MEDIAN (МЕДИАНА), QUARTILE (КВАРТИЛЬ), PERCENTILE (ПЕРСЕНТИЛЬ). Синтаксис MEDIAN (x) Возвращает выборочную медиану для выборки x.. QUARTILE (x, quart=0|1|2|3|4) Возвращает выборочный квартиль для выборки x. в зависимости от значения аргумента quart
PERCENTILE (x, k) Возвращает k-ый выборочный перцентиль для выборки x. Значения аргумента: 0≤k≤1. 3.8. Выборочная функция распределения и гистограммаВыборочная (или эмпирическая) функция распределения – это неубывающая функция FI(x), которая равна нулю при x<x(1) и равна 1 при x≥x(I). Между этими двумя точками функция FI(x) ступенчато возрастает на величину 1/I каждый раз при переходе через следующую точку x(i) –
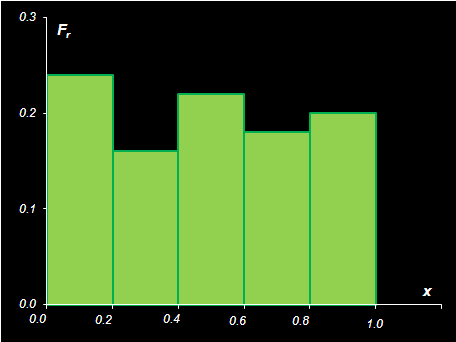
Выборочная функция распределения имеет важное теоретическое значение, т.к. при увеличении объема выборки I эмпирическая функция сходится к истинной функции распределения. Однако в практических приложениях чаще используется гистограмма. Для построения гистограммы область изменения выборочных значений [x(1), x(I)] разбивается на R частей равного размера. Затем подсчитывается, сколько элементов выборки попало в каждую из этих областей: I1+ I2+ …+ IR=I. После этого частоты Fr=Ir/I откладывают на ступенчатом графике, аналогичном показанному на Рис. 14.
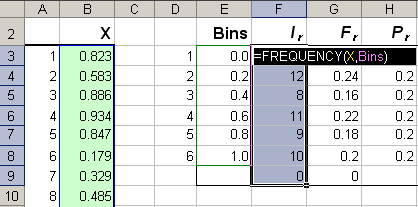
Рис.14 Гистограмма Для построения гистограмм в Excel применяется стандартная функция FREQUENCY (ЧАСТОТА). . Синтаксис FREQUENCY (data_array, bins_array) Возвращает число попаданий значений data_array в интервалы, заданные аргументом bins_array. Эта функция возвращает вертикальный массив, и она должна вводится как формула массива – с помощью комбинации клавиш . Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве bins_array. Дополнительный элемент содержит количество значений из data_array больших, чем максимальное значение в массиве bins_array. Рис.15 Пример использования функции FREQUENCY 3.9. Метод моментовВсе рассмотренные выше методы анализа выборок не учитывали конкретный вид распределения, из которого эта выборка была извлечена. Такие способы оценивания называются непараметрическими. Теперь мы рассмотрим типичный параметрический метод моментов. Пусть выборка x=(x1,…, xI) подчиняется функции распределения xi ~ F(x | p), которая известна с точностью до значений параметров p
=(p1,…, pM). Для оценки параметров
вычислим M выборочных моментов
из которой нужно численно найти значения оценок параметров p. Для примера рассмотрим случайную величину X=aY, где величина Y распределена по хи-квадрат Y ~ χ2(N). По выборке x=(x1,…, xI) нужно найти оценки двух неизвестных параметров a и N. E(X)=a E(Y)=aN, V(X)=a2V(Y)=2a2N. Поэтому
3.10. Метод максимума правдоподобияСамый популярный способ параметрического оценивания – это метод максимума правдоподобия. Учитывая, что каждый элемент выборки x=(x1,…, xI) имеет одну и ту же плотность вероятности f(xi | p), совместная плотность всей выборки имеет вид
Функция L(x|p) называется функцией правдоподобия выборки. Она зависит от двух групп переменных – выборочных значений x=(x1,…, xI), известных из эксперимента, и параметров p =(p1,…, pM), которые предстоит оценить. В качестве оценок берутся такие значения параметров p, при которых функция правдоподобия (или ее логарифм) имеет максимум
Рассмотрим, для примера, оценки параметров нормального распределения N(m, σ2). Из уравнений (3) и (6) следует, что
Максимум этой функции достигается при следующих значениях параметров
Таким образом, для нормального распределения оценки МП совпадают с выборочными оценками (8) и (10). 4. Свойства оценок4.1. СостоятельностьЛюбая оценка p(x) параметра p есть статистика, т.е. случайная величина. И как всякая случайная величина она обладает собственной функцией распределения, математическим ожиданием, дисперсией и т.д. Все эти характеристики позволяют сравнивать разные оценки, судить об их свойствах и качествах. Ниже следует краткий обзор основных свойств оценок. Оценка p(x) называется состоятельной, если она сходится по вероятности к значению оцениваемого параметра p при безграничном возрастании объема выборки I. Точнее, статистика p(x) является состоятельной оценкой параметра p тогда и только тогда, когда для любого положительного числа ε справедливо
Большинство оценок, используемых в практических приложениях, являются состоятельными. 4.2. СмещенностьОценка p(x) называется несмещенной, если E[p(x)]=p. Смещенные оценки часто встречаются в приложениях. Например, МП-оценка дисперсии нормального распределения (14) является смещенной
Для несмещенных оценок мерилом их точности является дисперсия V[p(x)] – чем она меньше, тем лучше. Для смещенных оценок нужно использовать математическое ожидание квадрата смещения d(x)= E[p(x) – p)2] . Имеет место формула
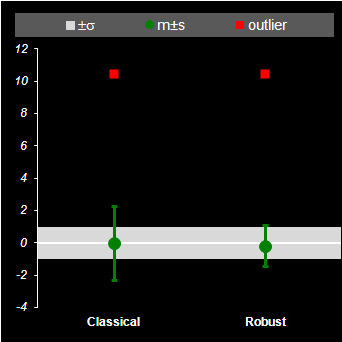
4.3. ЭффективностьНесмещенная оценка называется эффективной, если она имеет наименьшую возможную дисперсию. Оценки (14) нормального распределения являются эффективными, но вот выборочная оценка медианы (см. раздел 3.7) таковой не является – она менее эффективно оценивает m, чем выборочное среднее. Смещенные оценки могут оказаться более точными, чем несмещенные. Это означает, что часто можно построить такие смещенные оценки, для которых квадрат ошибки меньше, чем наименьшая эффективная дисперсия. На этом принципе основаны такие методы оценивания как PCR, PLS и др. 4.4. РобастностьРобастность оценки – это важная характеристика, которая, однако, плохо поддается формализации. Оценка p(x) называется робастной, если она устойчива к наличию выбросов в выборке. Как правило, эффективные оценки являются менее робастными, чем неэффективные. Выбирая более устойчивую оценку, мы расплачиваемся за это эффективностью. Для нормального распределения робастной оценкой среднего значения является медиана, а для СКО можно использовать MAD-оценку
в которой median рассчитывается по формуле (12). На листе Robust приведено сравнение классических и робастных оценок для выборки из стандартного нормального распределения N(0,1), в которой первый элемент заменен на выброс – случайную величину из распределения N(0,100). Рис.16 Обычные и робастные оценки 4.5. Нормальная выборкаЕсли выборка x=(x1,…, xI) извлечена из нормального распределения xi ~ N(m, σ2) ,
и оценки
5. Доверительное оценивание5.1. Доверительная областьВо многих случаях, помимо точечных оценок неизвестных параметров распределения, желательно указать область, в которой истинные значения этих параметров содержатся с заданной вероятностью. Такая область называется доверительной. Дадим точное определение. Пусть выборка x=(x1,…, xI) подчиняется функция распределения F(x | p), т.е. xi ~ F(x | p), которая известна с точностью до значений параметровp =(p1,…, pM). Статистика P(x) ∈ RM называется доверительной областью, соответствующей доверительной вероятности γ, если Pr{p ∈ P(x)}≥γ . 5.2.Доверительный интервалЧасто для каждого параметра pm строится своя одномерная область – доверительный интервал. Границы доверительного интервала – это две статистики p–(x) и p+(x), такие, что Pr{ p–(x) ≤ p ≤ p+(x)}≥γ. Для односторонних доверительных интервалов соответствующая граница заменяется на –∞, 0, или +∞. В большинстве практических случаев доверительные интервалы строятся для (асимптотически) нормальных выборок с помощью соотношений, приведенных в разделе 4.5. 5.3. Пример построения доверительного интервалаПриведем пример построения доверительного интервала. Пусть имеется выборка x=(x1,…, xI) из нормального распределения N(m, σ2) с известной дисперсией σ2. Построим доверительный интервал для параметра m – математического ожидания. Из уравнения (16) следует, что
где Φ–1 – квантиль стандартного нормального распределения, поэтому
Для построения симметричного доверительного интервала с доверительной вероятностью γ, положим α1= α2 = 0.5(1+γ). Для построения односторонних доверительных интервалов, положим α1= 1, α2 =γ, или α1= γ, α2 =1. 5.4. Вычисление доверительного интервала для нормального распределенияИспользуя соотношения, приведенные в разделе 4.5, можно построить доверительный интервал для параметров нормального распределения N(m, σ2). Пусть оценки Доверительный интервал для среднего значения m при неизвестной дисперсии σ2 имеет вид
где T–1(α | I–1) – квантиль распределения Стьюдента с I–1 степенями свободы. Доверительный интервал для дисперсии σ2 при известном среднем значении m имеет вид
где χ–2(α | I) – квантиль распределения хи-квадрат с I степенями свободы. Доверительный интервал для дисперсии σ2 при неизвестном среднем значении m имеет вид
где χ–2(α | I–1) – квантиль распределения хи-квадрат с I–1 степенями свободы. 6. Проверка гипотез6.1. Постановка задачиСтатистической гипотезой называется непротиворечивое утверждение, касающееся вида распределения имеющейся выборки. Основная гипотеза, нуждающаяся в проверке называется нулевой или нуль-гипотезой. Любая другая гипотеза, относительно которой проверяют нуль-гипотезу, называется альтернативой. Например: пусть имеется выборка из распределения хи-квадрат с N степенями свободы. Нуль-гипотеза состоит в том, что – H0: N=2 , альтернатива – H1: N>2 . На практике альтернативу часто опускают, формулируя только нуль-гипотезу. Гипотеза называется простой, если она однозначно определяет функцию распределения выборки. В противном случае гипотеза называется сложной. В примере: H0 – это простая гипотеза, а H1 – это сложная альтернатива. Гипотезы бывают параметрическими, когда вид распределения известен заранее, с точностью до численных значений его параметров – как в примере выше. Кроме того, гипотезы могут быть непараметрическими. Например: пусть имеется выборка из неизвестного распределения F. Нуль-гипотеза состоит в том, что – H0: F – это равномерное распределение. 6.2. Проверка гипотезМетод проверки статистической гипотезы называется статистическим критерием. Он строится на основе имеющейся выборки x=(x1,…, xI) с помощью измеримой функции S(x), называемой статистикой критерия. В пространстве значений статистики S(x) выбирается область C, называемая критической. Если S(x) ∈ С, то гипотезу отклоняют (отвергают), в противном случае – принимают. Статистика S(x) должна быть устроена особым образом – так, чтобы ее распределение не зависело от неизвестных параметров распределения выборки x. Кроме того функция распределения S(x) должна быть табулирована заранее. В большинстве практических приложений статистика S(x) строится из соображений нормальности. 6.3. Ошибки 1-го и 2-го родовПроверка статистической гипотезы не дает ее логического подтверждения или опровержения. Проверка только утверждает, что "имеющиеся данные (не) противоречат» выдвинутому предположению". Поэтому при проверке статистической гипотезы возможны случайные ошибки, которые могут быть двух родов. Ошибка 1-го рода происходит тогда, когда нуль-гипотеза верна, но отвергается согласно критерию. Ошибка 2-го рода происходит тогда, когда нуль-гипотеза не верна, но принимается согласно критерию. Вероятность ошибки первого рода называется уровнем значимости и обозначается α. Обычно уровень значимости выбирается равным 0.01, 0.05, или 0.1 и по этому значению подбирают критическую область Cα. 6.4. Пример проверки гипотезыПусть имеется выборка x=(x1,…, xI) из нормального распределения – xi ~ N(m, σ2) с известной дисперсией σ2 и неизвестным средним m. Проверяется простая нуль-гипотеза – H0: m=0. Альтернативу мы сформулируем позже. В качестве статистического критерия возьмем функцию
которая при m=0 подчиняется стандартному нормальному распределению – S ~ N(0, 1) . При заданном уровне значимости α критическая область определяется условием – Pr{|S|> Cα }= α . Поэтому Cα = Φ–1(1– α/2). Введем теперь альтернативную гипотезу – H1: m=a , и найдем величину ошибки 2-го рода. Ее величина β=Pr{|S|< Cα | m=a} рассчитывается при условии S ~ N(а, 1). Поэтому, β=Φ(Cα –a) – Φ(–Cα –a) . На листе Hypothesis приведены расчеты этого примера. Рис.17 Ошибки 1-го и 2-го родов при проверке гипотез 6.5. Критерий согласия хи-квадратКритерий согласия хи-квадрат проверяет соответствие между теоретическими вероятностями P1, P2, …и их эмпирическими частотными оценками I1/I, I2/I,… Для примера рассмотрим выборку x=(x1,…, xI) из неизвестного распределения – xi ~ F(x). Нуль гипотеза состоит в конкретизации этого распределения, т.е. в утверждении типа «F – это нормальное распределение с нулевым средним и дисперсией равной 2» В соответствие с выбранным гипотетическим распределением, область изменения случайной величины X, разбивается на R классов (корзин) и рассчитываются теоретические вероятности P1, P2, …, PR попадания в каждую из корзин. С другой стороны определяется, сколько элементов выборки попало в каждую из этих корзин – I1, I2, …, IR и вычисляются эмпирические вероятности Fr=Ir/I. Статистикой критерия согласия служит случайная величина
которая при I → ∞ стремится к распределению хи-квадрат с R–1 степенями свободы. Число и размеры корзин надо выбирать так, чтобы IPr > 6 . Критическая область на уровне значимости α определяется условием – S > χ–2(1–α | R–1) . Критерий согласия хи-квадрат можно применять и в том случае, когда теоретическое распределение F(x | p) известно с точностью до неизвестных параметров p =(p1,…, pM). Эти параметры предварительно оцениваются по той же выборке x и подставляются в функцию F(x | p). В этом случае следует изменить число степеней свободы на R–M–1. Для проверки согласия по критерию хи-квадрат в Excel применяется стандартная функция CHITEST (ХИ2ТЕСТ). . Синтаксис CHITEST(actual_range, expected_range) Вычисляет статистику S по формуле (17) используя actual_range= (I1, I2, …, IR) и expected_range= (IP1, IP2,…, IPR). Возвращает вероятность P= 1 – χ2(S | R–1). Для принятия гипотезы на уровне значимости α необходимо, чтобы P>1–α . Рис.18 Пример проверки критерия согласия хи-квадрат 6.6. F-критерийЭтот критерий применяется для проверки нуль-гипотезы о равенстве дисперсий в двух нормальных выборках: x=(x1,…, xI) и y=(y1,…, yJ). Пусть
– суть оценки выборочных дисперсий, найденные по формуле (9). Если
то обозначим
Иначе –
Статистикой F-критерия служит случайная величина
которая подчиняется распределению Фишера с N1, N2 степенями свободы. Критическая область на уровне значимости α определяется условием – S > F–1(1–α | N1, N2) . F-критерий очень чувствителен к нарушению предположения о нормальности распределений выборок, поэтому его не рекомендуется применять в практических приложениях. Для проверки F-критерия в Excel применяется стандартная функция FTEST (ФТЕСТ). Синтаксис FTEST(x, y) Возвращает вероятность P= 2[1 – F(S | N1, N2)]. Для принятия гипотезы на уровне значимости α необходимо, чтобы P>2α . Рис.19 Пример проверки F-критерия 7. Регрессия7.1. Простейшая регрессияВ простейшей постановке в регрессионном анализа рассматриваются две выборки: детерминированных величин x=(x1,…, xI) и случайных величин y=(y1,…, yI). Набор x называется предикторами, а набор y – откликами. Предполагается, что между этими величинами существует линейная связь вида yi=axi+b+εi, где a и b – неизвестные параметры, а εi – ошибки, т.е. некоррелированные случайные величины, имеющие нулевое мат.ожидание и неизвестную дисперсию σ2. Если дополнительно предположить, что ошибки распределены нормально
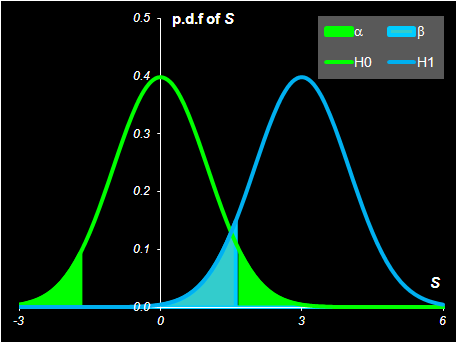
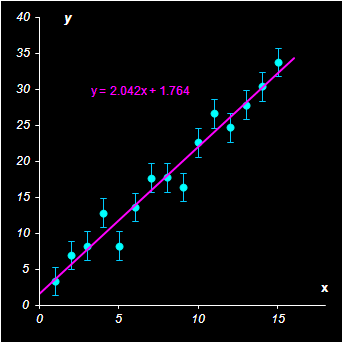
то оценивание параметров a и b методом МП сведется к поиску минимума следующей суммы квадратов Рис.20 Простая регрессия 7.2. Метод наименьших квадратовНа практике допущение о нормальности является избыточным и метод наименьших квадратов применяют и в случае ошибок произвольного вида. Минимум суммы Q достигается в точке –
Дисперсии оценок параметров равны –
Оценка параметра σ2 равна –
Если верно (18), то выполняются следующие соотношения
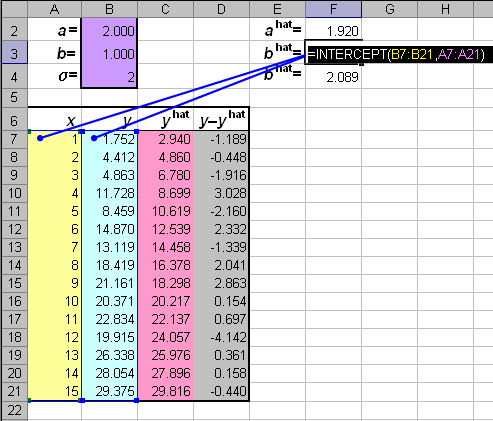
Кроме того, оценки параметров a и b независимы от оценки σ2 , что позволяет строить для оценок параметров доверительные интервалы с помощью статистики Стьюдента. Для вычисления параметров регрессии в Excel используют две стандартные функции: SLOPE (НАКЛОН) и INTERCEPT (ОТРЕЗОК) . Синтаксис SLOPE (known_y's=y, known_x's=x) Возвращает оценку параметра a. INTERCEPT (known_y's=y, known_x's=x) Возвращает оценку параметра b. Рис.21 Пример вычисления параметров линейной регрессии 7.3. Множественная регрессияЕстественным обобщением простой однофакторной регрессии является множественная регрессия – y=Xa+ε , в которой рассматривается связь между вектором откликов y и матрицей предикторов X. Обычное предположение относительно ошибок состоит в том, что E(εi)=0, cov(ε, ε)= σ2I , где I – единичная (I×I) матрица. Если в задаче имеется I наблюдений и J переменных, то матрица X имеет размерность I×J. Цель регрессионного анализа – найти оценки неизвестных коэффициентов a=(a1,…,aJ)t, такие, которые минимизируют сумму квадратов остатков –
В обычном методе наименьших квадратов (МНК) предполагается, что матрица XtX обратима. Тогда минимум Q(a) достигается при ahat=(XtX)–1Xty . Оценка параметра σ2 равна s2=Q(ahat)/(I–J). Матрица ковариаций оценок равна C=s2(XtX)–1 . Для построения множественной регрессии в Excel используют две стандартные функции: TREND (ТЕНДЕНЦИЯ) и LINEST (ЛИНЕЙН) применение которых разобрано в пособии Матричные операции в Excel. ЗаключениеСтатистические методы активно используются при анализе данных, в том числе и хемометрическими методами. Примеры приведены в пособиях
|
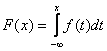 . .
. .
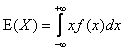 .
. 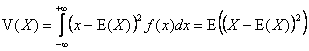 .
.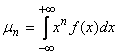 .
.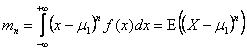 .
.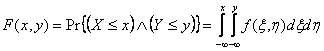 .
.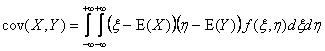 ,
,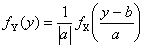 ,
,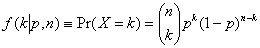 ,
,
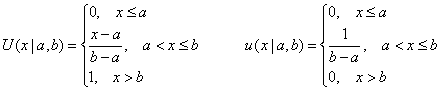
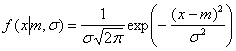
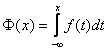
 .
.

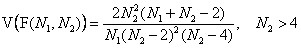 .
.
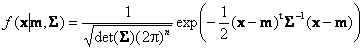 ,
,
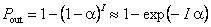 .
.
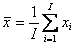 .
.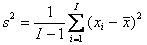 ,
,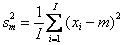 .
.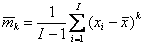 ,
,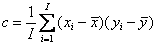 ,
,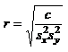 .
.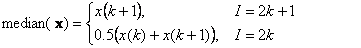 .
.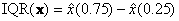 ,
, .
. 
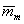
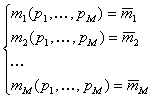 ,
,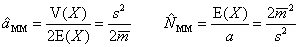 .
. 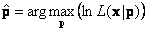 .
.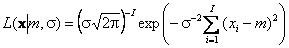 .
.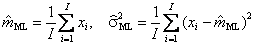 .
.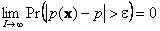 .
. 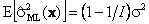 .
. 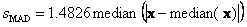 ,
, 
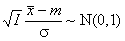
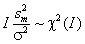 , т.е.имеет
распределение
, т.е.имеет
распределение 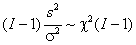 , т.е. имеет
распределение
, т.е. имеет
распределение 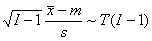 , т.е. имеет
распределение
, т.е. имеет
распределение 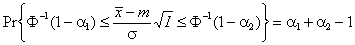 ,
,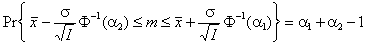 .
.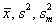 определены
формулами (
определены
формулами (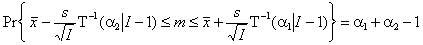 ,
,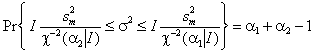 ,
,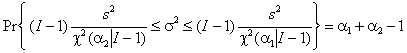 ,
,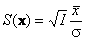 ,
,
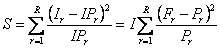 ,
,
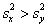
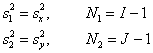 .
. .
. ,
,


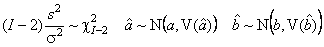 .
.
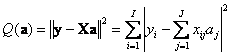 .
.