Калибровка (Градуировка)
Содержание
ВведениеВ этом пособии рассмотрены основные методы, применяемые для решения задач калибровки (называемой также градуировкой). Текст ориентирован, прежде всего, на специалистов в области анализа экспериментальных данных: химиков, физиков, биологов, и т.д. Он может служить пособием для исследователей, начинающих изучение этого вопроса. Продолжить исследования можно с помощью указанной литературы. В пособии интенсивно используются понятия и методы матричной алгебры – вектор, матрица, и т.п. Читателям, которые плохо знакомы с этим аппаратом, рекомендуется изучить, или, хотя бы просмотреть, пособие "Матрицы и векторы". Изложение иллюстрируется примерами, выполненными в рабочей книге Excel “Calibration.xls”, которая сопровождает этот документ. Предполагается, что читатель имеет базовые навыки работы в среде Excel, умеет проводить простейшие матричные вычисления с использованием функций листа, таких как МУМНОЖ, ТЕНДЕНЦИЯ и т.п. Освежить эти знания можно с помощью пособия Матричные операции в Excel. Важная информация о работе с файлом Calibration.xls Ссылки на примеры помещены в текст как объекты Excel. По форме эти примеры имеют абстрактный, модельный характер, однако, по своей сути, они тесно связаны с задачами, встречающимися на практике. 1. Базовые сведения1.1. Постановка задачиСуть задачи калибровки состоит в следующем. Пусть имеется некоторая переменная (свойство) y, величину которой необходимо установить. Однако, по ряду обстоятельств (недоступность, дороговизна, длительность), прямое измерение величины y невозможно. В то же время можно легко (быстро, дешево) измерить другие величины: x=(x1, x2, x3,…), которые связаны с искомой величиной y. Задача калибровки состоит в установлении количественной связи между переменными x и откликом y – y=f(x1, x2, x3,…| a1, a2, a3,…) +ε На практике это означает:
Разумеется, калибровку нельзя построить абсолютно точно. В дальнейшем мы увидим, что это не только невозможно, но и опасно. В калибровочной зависимости всегда присутствуют погрешности (ошибки) ε, источник которых – пробоотобор, измерения, моделирование, и т.д. Простейший пример калибровки дает общеизвестный прибор, называемый безменом, т.е. пружинные весы. Искомая величина y – это вес образца, а x – это удлинение пружины весов. Закон Гука – y=ax + ε, связывает y и x через коэффициент жесткости пружины a, который априори неизвестен. Процедура калибровки очень проста – взвешиваем стандартный образец весом в 1 кг и отмечаем на шкале удлинение пружины, затем используем образец в 2 кг, и т.д. В результате этой калибровки (точнее, градуировки) получается шкала, по которой можно определить вес нового, нестандартного образца. Этот элементарный пример демонстрирует основные черты процедуры калибровки, которые подробно будут рассмотрены далее. Во-первых, для калибровки необходимы несколько стандартных образцов, для которых величины y известны заранее. Во-вторых, диапазон, в котором предполагается измерять показатель y, должен полностью покрываться этими калибровочными образцами. Действительно, нельзя измерять образцы весом более 5 кг, если в калибровке использовались образцы, весом менее чем 5 кг. Разумеется, на практике все обстоит не так просто, как в этом элементарном примере. Например, в калибровке может участвовать не один показатель y (отклик), а несколько откликов y1, y2,..... yK, которые нас интересуют. Все возможные особенности, различные трудности, сопутствующие процедуре калибровке будут рассмотрены далее. Сейчас же мы подведем первые итоги и сформулируем задачу калибровки в общем виде. Пусть имеется матрица Y, размерностью (I×K), где I – это число стандартных образцов (сравнения), использованных в калибровке, а K – это число одновременно калибруемых откликов. Матрица Y содержит значения откликов y, известные из независимых экспериментов (референтные или стандартные значения). Пусть, с другой стороны, имеется соответствующая матрица переменных X размерностью (I×J), где I – это, естественно, тоже число образцов, а J – это число независимых переменных (каналов), используемых в калибровке. Матрица X состоит из альтернативных, как правило, многоканальных (J>>1) измерений. Используя калибровочные данные (X, Y), требуется построить функциональную связь между Y и X. Рис. 1 Калибровочный набор данных Итак, задача калибровки состоит в построении математической модели, связывающей блоки X и Y, с помощью которой можно в дальнейшем предсказывать значения показателей y1, y2,..... yK, по новой строке значений аналитического сигнала x. 1.2. Линейная и нелинейная калибровкиТеоретически функциональная связь между переменными x и y может быть сложной, например, y=b0 exp(b1x+b2x2) + ε . Однако на практике большинство используемых калибровок являются линейными, т.е. имеют вид – y=b0 + b1x1 + b2x2+...+ bJxJ + ε . Заметим, что термин "линейность" употребляется в контексте этого пособия вместо более правильного термина "билинейность", означающего линейность как по отношению к переменным x, так и в отношении коэффициентов b. Поэтому, калибровка y=b0 + b1x + b2x2 + ε . является нелинейной, несмотря на то, что она легко "линеаризуется" введением новой переменной x2=x2. Главное преимущество билинейной модели – это единственность, тогда как все прочие калибровки образуют бесконечное множество, выбор из которого затруднителен. В этом пособии рассматриваются только линейные калибровки вида – Читатели, заинтересованные в изучении нелинейных методов анализа данных могут обратиться к описанию программы Fitter. Предпочтение (би)линейных, формальных моделей, не отягощенных дополнительным физико-химическим смыслом, является магистральным направлением развития хемометрики. Такой подход позволяет исключить влияние субъективного фактора, проявляющегося при выборе калибровочной зависимости. Однако за это приходится расплачиваться – все линейные модели имеют ограниченную область применения.
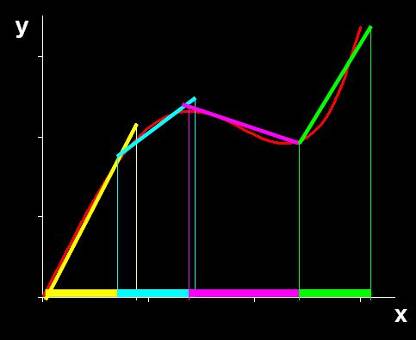
Рис. 2 Линеаризация калибровки Суть дела иллюстрирует Рис. 2, где показаны четыре участка, на которых сложная нелинейная зависимость приближается простыми линейными моделями. Каждая из этих моделей работает только на своей области переменной x и выход за ее границы приводит к грубым ошибкам. Принципиальным моментом здесь является то, какую область можно считать допустимой – иначе говоря, насколько широко можно применять калибровочную модель. Ответ на этот вопрос дают методы проверки (валидации). 1.3. Калибровка и проверкаПри надлежащем построении калибровочной модели исходный массив данных состоит из двух независимо полученных наборов, каждый из которых является достаточно представительным. Первый набор, называемый обучающим, используется для идентификации модели, т.е. для оценки ее параметров. Второй набор, называемый проверочным, служит только для проверки модели. Построенная модель применяется к данным из проверочного набора, и полученные результаты сравниваются с проверочными значениями. Таким образом принимается решение о правильности, точности моделирования методом тест-валидации.
Рис. 3 Обучающий и проверочный наборы В некоторых случаях объем данных слишком мал для такой проверки. Тогда применяют другой метод – перекрестной проверки (кросс-валидация, скользящая проверка). В этом методе проверочные значения вычисляют с помощью следующей процедуры. Некоторую фиксированную долю (например, первые 10% образцов) исключают из исходного набора данных. Затем строят модель, используя только оставшиеся 90% данных, и применяют ее к исключенному набору. На следующем цикле исключенные данные возвращаются, и удаляется уже другая порция данных (следующие 10%), и опять строится модель, которая применяется к исключенным данным. Эта процедура повторяется до тех пор, пока все данные не побывают в числе исключенных (в нашем случае – 10 циклов). Наиболее (но неоправданно) популярен вариант перекрестной проверки, в котором данные исключаются по одному (Leave-One-Out – LOO).
Рис. 4 Метод перекрестной проверки Используется также проверка методом корректировки размахом, суть которой предлагается изучить самостоятельно по книгам. 1.4. "Качество" калибровкиРезультатом калибровки являются
величины
Рис. 5 Остатки в обучении и в проверке Следующие величины характеризуют "качество" калибровки в среднем.
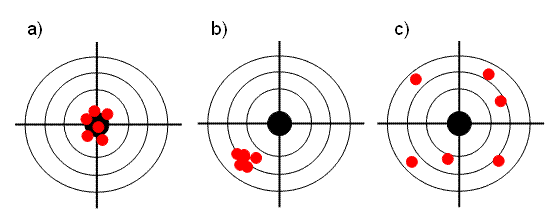
Во всех этих формулах величины eki – это элементы матриц Ec или Et. Для характеристик, наименование которых оканчивается на C (например, RMSEC), используется матрица Ec (обучение), а для тех, которые оканчиваются на P (например, RMSEP), берется матрица Et (проверка). 1.5. Неопределенность, точность и воспроизводимостьТакое большое число показателей, характеризующих качество калибровки, объясняется не только историческими причинами, но и тем, что они отражают различные свойства неопределенности при обучении, и при проверке (прогнозе). Для объяснения этих показателей необходимо ввести понятия воспроизводимости (прецизионности) и точности. Воспроизводимость (precision) характеризует то, насколько близко находятся друг от друга независимые повторные измерения. Точность (accuracy) определяет степень близости оценок к истинному (стандартному) значению y.
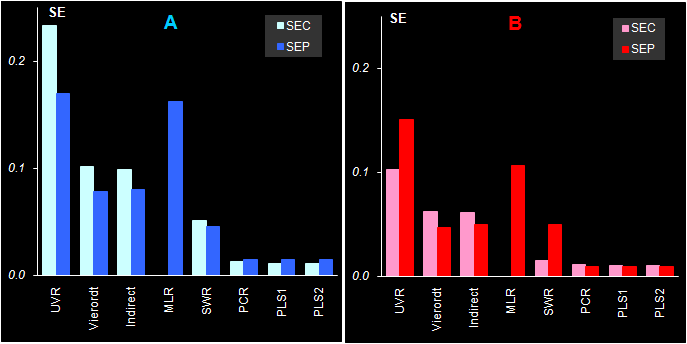
Рис.6 Точность и воспроизводимость Рис. 6 объясняет суть дела. Графики a) и b) представляют оценки с хорошей воспроизводимостью. Вариант a) , кроме того, обладает и высокой точностью, что, разумеется, нельзя сказать о графике c). В последнем случае и воспроизводимость, и точность оставляют желать лучшего. Показатели SEC и SEP характеризуют воспроизводимость калибровки, тогда как RMSEC и RMSEP показывают ее точность. Величины BIASC и BIASP определяют смещение калибровки относительно истинного значения (Рис. 6b). Можно показать, что –
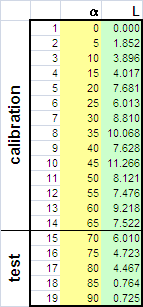
Таким образом, при построении калибровки предпочтение следует отдавать показателям RMSE, а не SE. Показатели TRV и ERV характеризуют ситуацию "в целом", без различения калибруемых откликов, т.е. 1.6. Недооценка и переоценкаПри построении калибровки исследователь часто имеет возможность последовательного усложнения модели. Приведем простейший пример, иллюстрирующий этот процесс. Из курса школьной физики известно, что расстояние L, на которое летит снаряд, выпущенный со скоростью v из орудия, наклоненного под углом α к горизонту, равно – L=v2sin(2α)/g. Предположим, что у нас имеются экспериментальные данные L(α ).
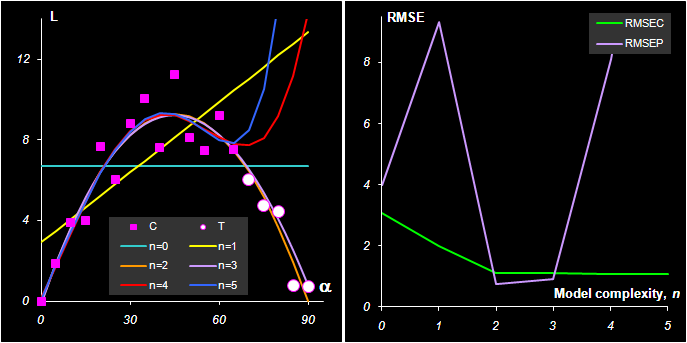
Рис.7 Данные для артиллерийского примера Забудем о том, что функциональная связь между L (т.е., y) и α (т.е., x) нам известна, и попробуем построить формальную полиномиальную калибровку – L=b0 + b1α + b2α2 +…. bn αn + ε по этим данным. На Рис. 8а
показано, как описываются обучающие (
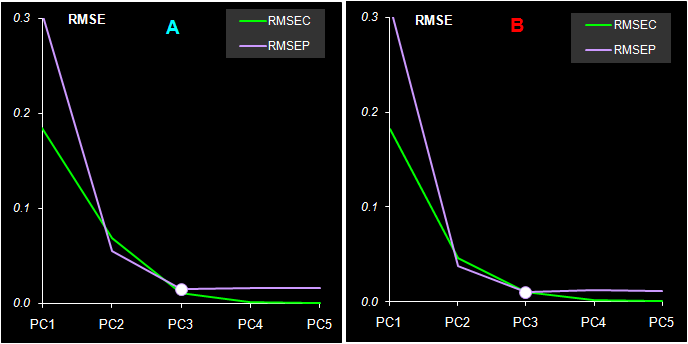
Рис.8
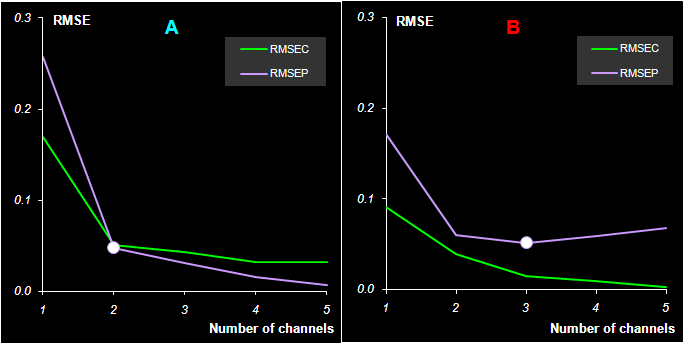
Артиллерийский пример. На Рис. 8b показано, как изменяются показатели RMSEC и RMSEP при увеличении сложности модели. Это – типичный график, в котором RMSEC монотонно падает, а RMSEP проходит через минимум. Именно точка минимума RMSEP позволяет определить оптимальную сложность модели. В нашем случае – это 2. Теперь мы можем вспомнить о содержательной модели, которая хорошо аппроксимируется полиномом второй степени по α – L=v2/g sin(2α) ≈ Const α(α – π/4) В задачах многомерной калибровки недооценка и переоценка проявляются через выбор числа скрытых, главных компонент. Когда их число мало, модель плохо приближает обучающий набор и при увеличении сложности модели RMSEC монотонно уменьшается. Однако качество прогноза на проверочный набор может при этом ухудшаться (U-образная форма RMSEP). Точка минимума RMSEP, или начало плато, соответствует оптимальному числу главных компонент. Проблема сбалансированности описания данных рассматривается во многих работах А. Хоскюлдссона, который в 1988 году ввел новую концепцию моделирования – так называемый H-принцип. Согласно этому принципу точность моделирования (RMSEC) и точность прогнозирования (RMSEP) связаны между собой. Улучшение RMSEC неминуемо влечет ухудшение RMSEP, поэтому их нужно рассматривать совместно. Именно по этой причине множественная линейная регрессия, в которой всегда участвует явно избыточное число параметров, неизбежно приводит к неустойчивым моделям, непригодным для практического применения. 1.7. МультиколлинеарностьРассмотрим задачу множественной линейной калибровки Разумеется, здесь мы имеем дело с обучающим набором данных. Мы не пишем индекс у матриц (Yс, Xс) только для простоты обозначений. Классическое решение этой задачи находится с помощью метода наименьших квадратов. Минимизируя сумму квадратов отклонений (Y – XB)t(Y – XB), получаем оценки неизвестных коэффициентов B – Далее находится – – оценка искомых откликов. Главная проблема при таком классическом подходе – это обращение матрицы XtX . Очевидно, что если число стандартных образцов меньше, чем число переменных (I<J) то то обратной матрицы не существует. Более того, даже при достаточно большом числе образцов (I>J), обратной матрицы может и не быть. Рассмотрим простейший пример.
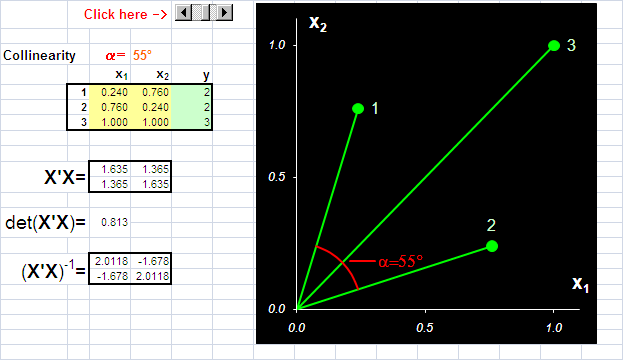
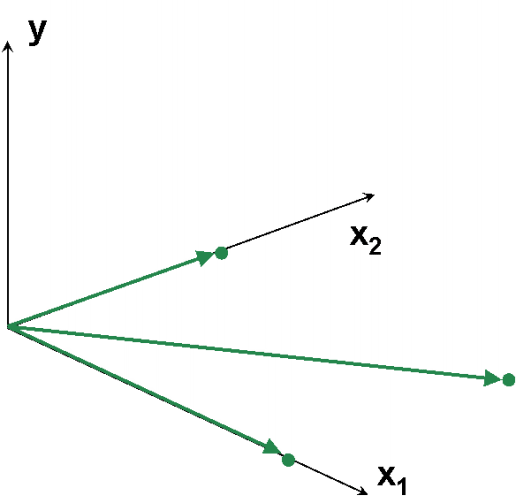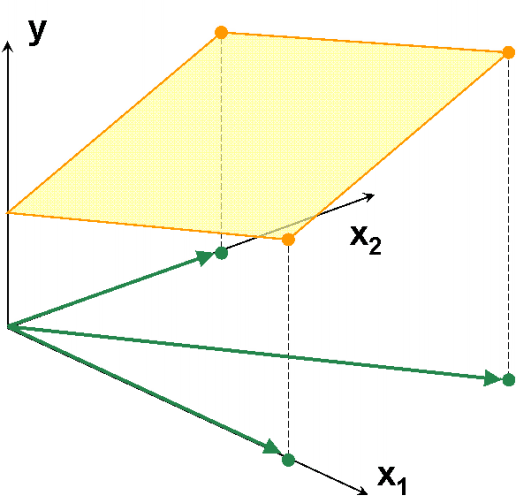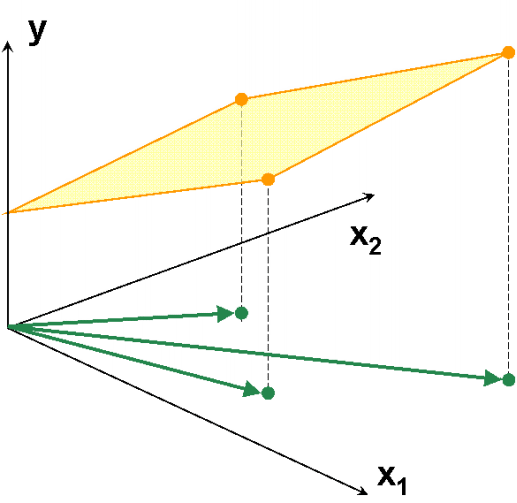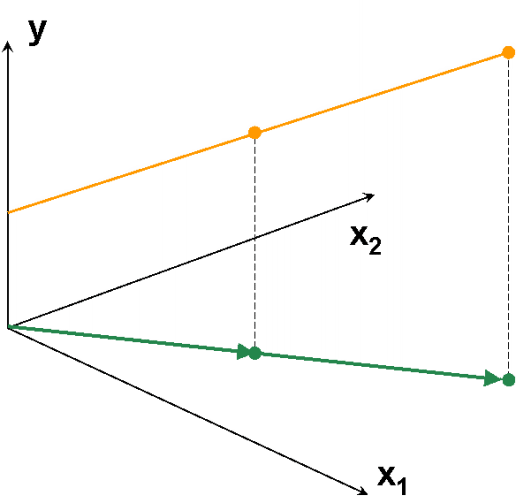
Рис.9 Пример коллинеарных данных На Рис. 9 представлены данные, в которых всего три образа (I=3) и две переменные (J=2). Используя активный элемент на листе, угол между векторами 1 и 2 можно изменять от 90о до 0о. Чем меньше угол, тем меньше детерминант матрицы XtX и тем хуже определяется матрица (XtX)–1. В предельном случае, когда угол между векторами равен 0о, матрица XtX не может быть обращена. При этом векторы 1 и 2 колинеарны, т.е. они лежат на одной прямой, совпадающей с вектором 3. Анимация на Рис. 10 иллюстрирует суть проблемы – невозможность построения калибровки классическим способом, когда данные коллинеарны.
Рис.10 Пример коллинеарных данных В многомерной калибровке (т.е. при J>> 1), мы все время сталкиваемся с мультиколлинеарностью – множественными связями между векторами X-переменных, приводящими к той же проблеме – невозможности обращения матрицы XtX. Далее мы увидим, что можно сделать в случае мультиколлинеарности данных. 1.8. Подготовка данныхВажным условием правильного моделирования и, соответственно, успешного анализа, является предварительная подготовка данных, которая включает различные преобразования исходных, "сырых" экспериментальных значений. Простейшими преобразованиями является центрирование и нормирование. Центрирование – это вычитание из исходной матрицы X матрицы M, т.е. Обычно усреднение проводится по столбцам: для каждого вектора xj вычисляется среднее значение –
Тогда M=(m11,..., mJ1), где 1 – это вектор из единиц размерности I. Центрирование – это почти обязательная процедура перед применением проекционных методов. Второе простейшее преобразование данных, нормирование, не является обязательным. Нормирование, в отличие от центрирования, не меняет структуру данных, а просто изменяет вес различных частей данных при обработке. Чаще всего применяется нормирование по столбцам – это умножение исходной матрицы X справа на матрицу W, т.е.
Матрица W – это диагональная матрица размерности J×J. Обычно диагональные элементы wjj равны обратным значениям стандартного отклонения –
вычисленным для каждого столбца xj. Нормирование по строкам (называемое также нормализацией) – это умножение матрицы X слева на диагональную матрицу W, т.е.
При этом размерность W равна I×I, а ее элементы wii – это обратные значения стандартных отклонений строк xit. Комбинация центрирования и нормирования по столбцам
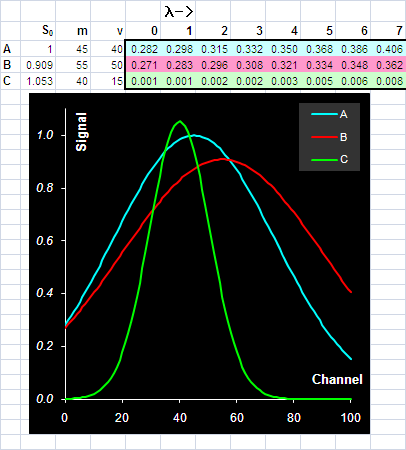
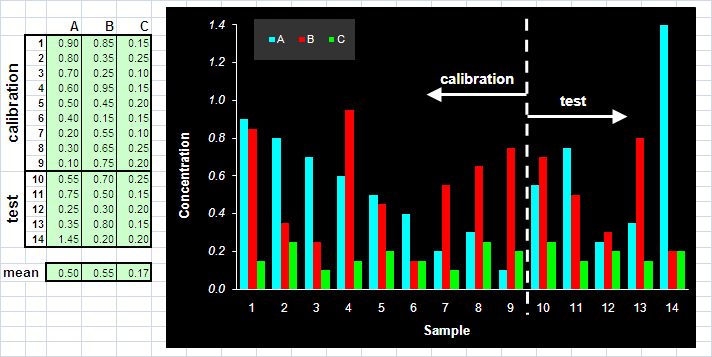
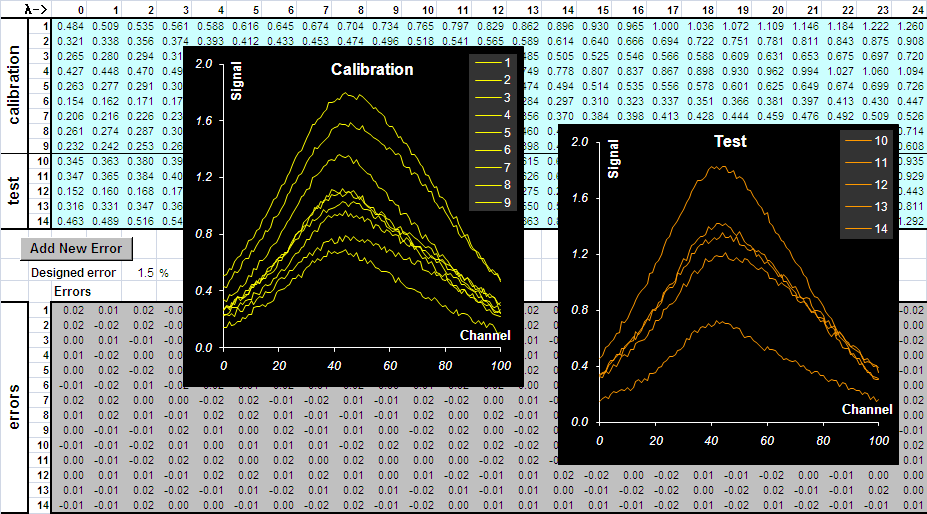
называется автошкалированием. Нормирование данных часто применяют для того, чтобы уравнять вклад в модель от различных переменных (например, в гибридном методе ЖХ-МС), учесть неравномерные погрешности, или для того, чтобы обрабатывать совместно разные блоки данных. Нормирование также можно рассматривать как метод, позволяющий стабилизировать вычислительные алгоритмы. В тоже время, к этому преобразованию нужно относиться с большой осторожностью, т.к. оно может сильно исказить результаты качественного анализа. Любое преобразование данных – центрирование, шкалирование, и т.п. – всегда делается сначала на обучающем наборе. По этому набору находятся значения mj и dj, которые затем применяются и к обучающему, и к проверочному набору 2. Модельные данные2.1. Принцип линейностиДля иллюстрации и сравнения различных методов калибровки будем использовать модельный пример, в котором "экспериментальные" данные мы создадим сами. Прообразом для этого примера служит популярная задача анализа спектральных данных. Известно, что в таких экспериментах хорошо выполняется принцип линейности. Пусть имеются два вещества A и B, смешанные в концентрациях cA и cB. Тогда спектр смеси есть – X = cA·SA+ cB·SB, где SA и SB – спектры чистых веществ. Заметим, что тот же принцип линейности выполняется и в хроматографии, где в роли "спектров" выступают хроматографические профили чистых компонент смеси. 2.2. "Чистые" спектрыДля моделирования "чистых" спектров S(λ) мы использовали гауссовы пики –
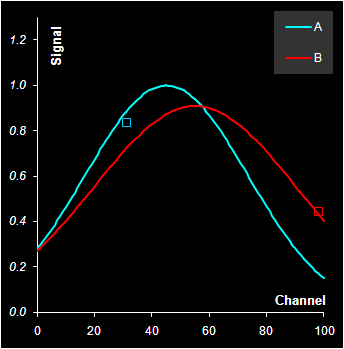
где S0, m, v – это параметры спектров, а λ = 0, 1, 2, …, 100 – это условный номер канала (длина волны, время удерживания, и т.п.). На Рис. 11 показаны спектры трех веществ: A, B и C, которые участвуют в примере. Вещества A и B – это искомые величины (отклики), а компонент C добавлен в систему как шум, т.е. нежелательная примесь.
Рис.11 Чистые спектры Видно, что спектры сильно перекрываются, особенно A и B, у которых нет участков, где бы присутствовал только один сигнал. Это обстоятельство сильно мешает построению калибровок классическими способами. Чистые спектры можно изменить, задавая новые величины в ячейках B4:D6, которые соответствуют параметрам формы гауссовых пиков. Например "растащить" спектры A и B так чтобы они мало перекрывались и посмотреть, что из этого получится. 2.3."Стандартные" образцыДля создания модельных данных мы должны задать концентрации всех компонентов в системе для различных образцов. Будем считать, что у нас имеется 14 образцов, из которых девять – это обучающий набор, а пять – это проверочный набор. Значения концентраций представлены на Рис. 12.
Рис.12 Концентрации в обучающем и проверочном наборах Заметим, что среди этих образцов нет ни одного "чистого", т.е. такого в котором все концентрации, кроме одной (например, A) , равны нулю. Это тоже "мешает" использованию традиционных методов калибровки. 2.4. Создание X данныхДля получения "экспериментальных спектров" надо матрицу концентраций C умножить на матрицу чистых спектров S и добавить к результату случайные ошибки (погрешности) – На Рис. 13 представлены полученные спектры в обучающем и проверочном наборах. Погрешности моделировались со стандартным отклонением 0.015.
Рис.13 Создание модельных данных Генерация случайных ошибок производится с помощью простого VBA макроса , который запускается кнопкой Add New Error. Величина желаемой погрешности (СКО) предварительно задается в ячейке E18 с именем RMSE, озаглавленной Designed error. Погрешность, которая получилась в результате генерации случайных чисел выводится в ячейку J18, озаглавленную Obtained error. Генерируя новые данные можно узнать много интересного о методах калибровки. 2.5. Центрирование данныхВ соответствие с концепцией, изложенной в разделе 1.8, данные нужно правильно подготовить. В рассматриваемом модельном примере нет необходимости в выравнивании переменных – все спектральные каналы имеют схожие величины сигналов. А вот центрирование, как спектров X, так и откликов Y , бывает необходимо для построения некоторых моделей. Для центрирования концентраций Y вычисляются средние по обучающему набору. Эти средние затем вычитаются из всех значений Y. Аналогично проводится и центрирование в данных X – вычисляются средние значения для каждого канала по обучающему набору и затем эти значения вычитаются из всех величин X – по столбцам. 2.6. Обзор данныхИтак, мы построили модельные данные (Y, X): концентрации – матрицу Y размером (14×2) и спектры – матрицу X размером (14×101). Исследуя эти данные, мы "забудем" (т.е. не будем использовать в расчетах) то, что в системе присутствует еще одно "скрытое" вещество C. Интересно, сможем ли мы обнаружить его присутствие? Кроме того, не будут использоваться и спектры чистых веществ A и B, примененные для построения данных. Мы постараемся их восстановить и сравнить с исходными спектрами. Все данные мы разделили на два блока: обучающий (или калибровочный) – 9 образцов, и проверочный (или тестовый) – 5 образцов. Мы будем строить калибровки с помощью разных методов, используя только первый, обучающий набор. Второй, проверочный набор послужит для оценки качества получаемых моделей. Данные используются для иллюстрации и сравнения различных методов калибровки. Они размещены в рабочей книге Excel с именем Calibration.xls.Эта книга включает в себя следующие листы: Intro: краткое введение Layout: схемы, объясняющая имена массивов, используемых в примере Gun: иллюстрация пере - и недооценки в калибровке Multicollinearity: иллюстрация проблемы мультиколлинеарности в калибровке Pure Spectra: истинные чистые спектры S Concentrations: истинные концентрационные профили C Data: модельные данные, используемые в примере.. UVR: одноканальная калибровка Vierordt: калибровка методом Фирордта Indirect: непрямая калибровка MLR: множественная линейная регрессия SWR: калибровка пошаговой реегрессией PCR: регрессия на главные компоненты PLS1: метод проекция на латентные переменные 1 PLS2: метод проекция на латентные переменные 2 Compare сравнение различных методов 3. Классическая калибровкаКлассическая калибровка опирается на использовании того же принципа линейности, по которому строились модельные данные, т.е. на уравнение (13) Здесь X=Xc и C=Yc – это обучающая часть исходных данных (не центрированных), а S – это матрица "чистых спектров" (она же матрица чувствительности). Если матрица S известна априори, то концентрации определяются так
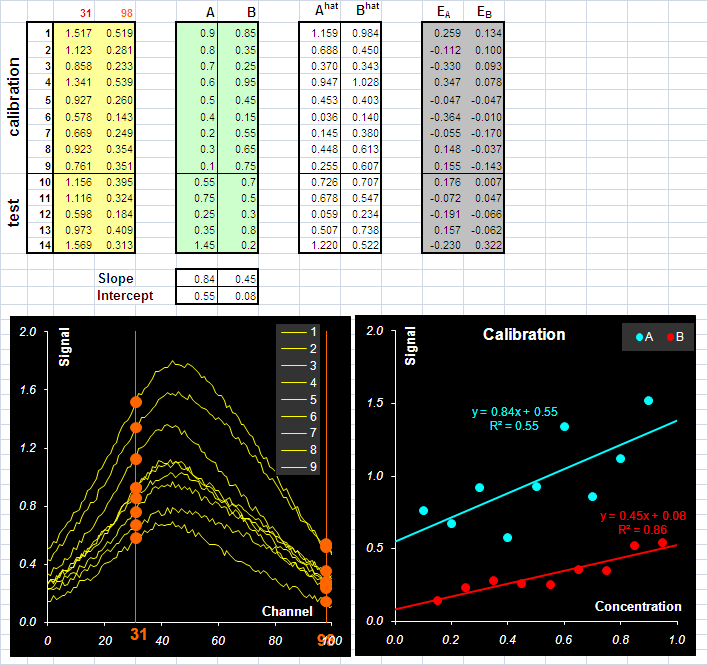
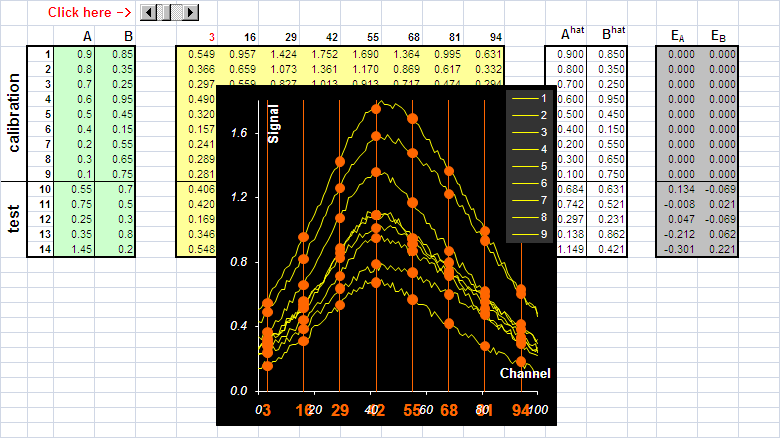
где S+ = =St(SSt)−1– это псевдообратная матрица. Этот случай называется прямой калибровкой. Однако, на практике матрица чистых спектров, как правило, неизвестна и ее приходится восстанавливать из обучающих данных. 3,1. Калибровка по одному каналу (однофакторная)Это самый простой, наивный вид калибровки. Если для каждого аналита из всех данных X выделить один канал (длину волны), то получится несколько векторов x. Тогда, используя обучающие данные, можно построить для каждого вещества простейшую одномерную регрессию – x=sc+b , одну для вещества A (c=cA), а другую для B (c=cB). Формулы для оценивания коэффициентов s (наклон)и b (отсечение) можно найти в любом пособии по линейной регрессии, например, здесь. В Excel это проще всего сделать с помощью функции ЛИНЕЙН (LINEST). После того, как эти коэффициенты найдены, значения концентраций можно вычислять по уравнению c=(x–b)/s На Рис.14 приведен пример построения двух этих регрессий для каналов 31 (A) и 98 (B). График показывает, как проходят линии регрессий для веществ A и B.
Рис.14 Калибровка по одному каналу) Обратите внимание, что в каждом калибровочном уравнении присутствует свободный член b. Это противоречит исходному уравнению (13), но зато позволяет учесть влияние фона, или, как в нашем случае, присутствие посторонней примеси (вещества C). Величины коэффициентов s (наклон) соответствуют значениям "чистых" спектров. На Рис. 15 показаны "чистые" спектры веществ A и B и соответствующие значения коэффициентов m.
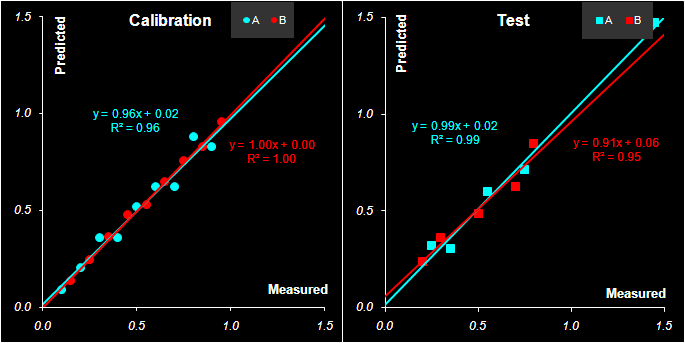
Рис.15 "Чистые" спектры и их оценки для выбранных каналов Для визуальной оценки качества
калибровки традиционно используются
графики "измерено-предсказано", в
которых по оси абсцисс откладываются
известные (стандартные) концентрации y,
а по оси ординат соответствующие им
величины оценок
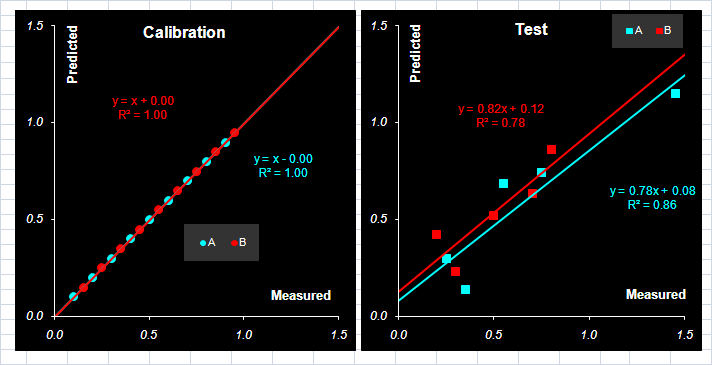
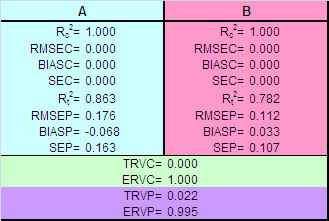
Рис.16 Графики "измерено-предсказано" для однофакторной калибровки. Обучающий и проверочный наборы В Табл. 1 приведены характеристики качества однофакторной калибровки веществ A и B, вычисленные в соответствие с формулами раздела 1.4. Табл. 1 Характеристики качества однофакторной калибровки
Разумеется одномерную калибровку можно проводить по любому каналу. На листе UVR для этого достаточно изменить значения в ячейках C2 и D2, которые соответствуют двум каналам – для веществ A и B. и проверить как меняется качество калибровки. Так наилучшее значение RMSEP=0.173 для вещества A достигается при калибровке по 31 каналу, а наихудшее значение RMSEP=0.702 получается при λ =97. Соответственно для вещества B имеем: наилучшее значение RMSEP=0.151 для λ =98 и наихудшее RMSEP=0.611 для λ =20. Существует мнение, что калибровку лучше проводить в точке, где соответствующий "чистый спектр" имеет максимум. Из рассмотренного примера видно, что это не так. В точке λ =45 (максимум A) RMSEP=0.205, а в точке λ =55 (максимум B) RMSEP=0.484. 3.2. Метод ФирордтаВпервые задача анализа спектрофотометрических данных
была рассмотрена в работе Карла фон Фирордта (Karl
von Vierordt Метод Фирордта похож на метод одноканальной калибровки. В нем также выбирается по одному каналу для каждого вещества, но регрессионные уравнения рассматриваются не независимо, а совместно
Здесь матрица
Для оценки матрицы чувствительности S умножим это уравнение слева на транспонированную матрицу концентраций Yc
Тогда матрица –
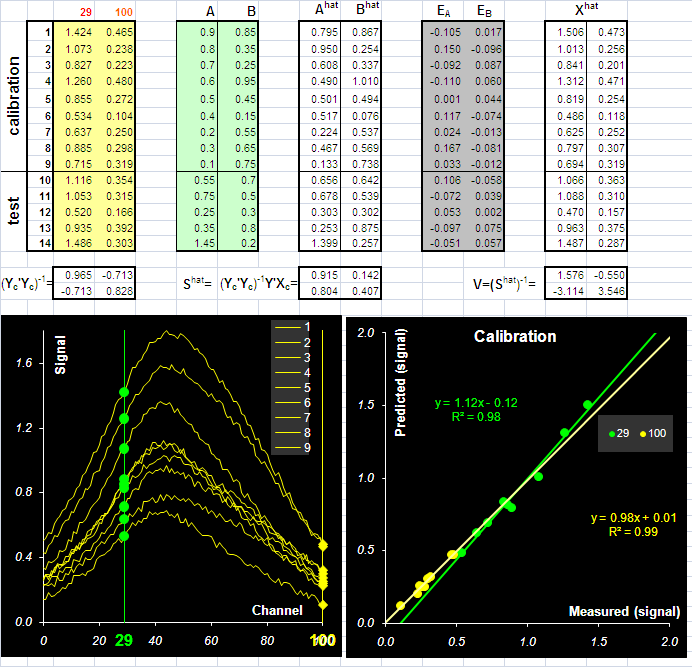
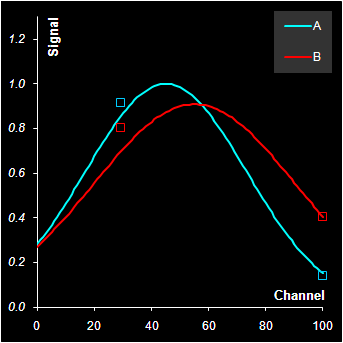
будет оценкой матрицы чувствительности. На Рис. 17 показано применение метода Фирордта для модельного примера, где для калибровки выбраны два канала 29 и 100.
Рис.17 Применение метода Фирордта График "предсказано-измерено" представляет результаты калибровки сигнала (спектров x) для выбранных каналов. Элементы матрицы чувствительности S соответствуют значениям матрицы "чистых" спектров. На Рис. 18 показано это соответствие.
Рис.18 Элементы матрицы чувствительности S (точки) в методе Фирордта и "чистые" спектры Для оценки и предсказания значений концентрации веществ A и B. нужно вычислить матрицу обратную к матрице чувствительности S. Сделать это просто, т.к. эта матрица квадратная. Тогда матрица V
будет линейным "оценивателем"
матрицы концентраций Y. Для того,
чтобы найти оценки величин
концентраций в обучающем наборе, надо
матрицу V умножить на матрицу
соответствующих спектров
Аналогично, для оценки концентраций в проверочном наборе, матрица V умножается на Xt –
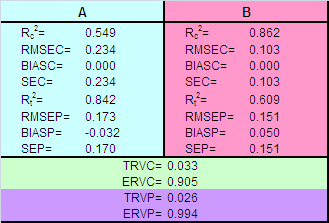
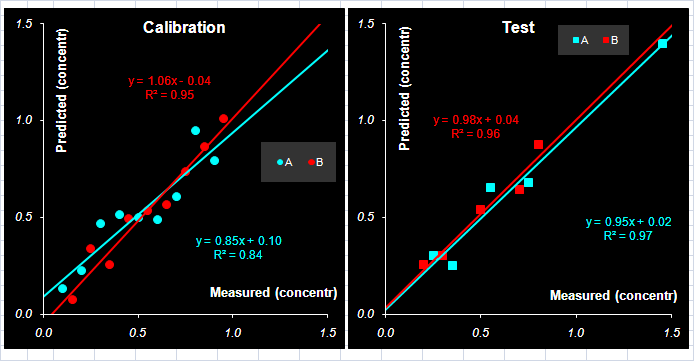
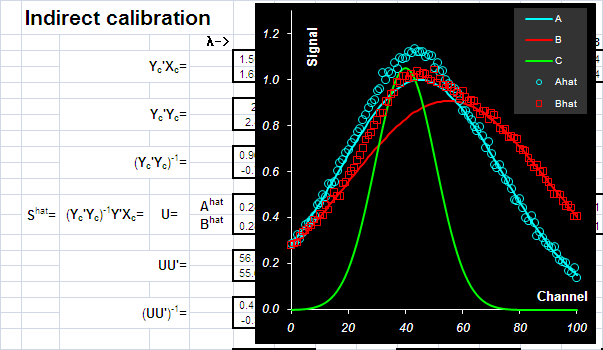
Графики "предсказано-измерено" показаны на Рис. 19
Рис.19 Графики "измерено-предсказано" для метода Фирордта. Обучающий и проверочный наборы В Табл. 2 приведены характеристики качества калибровки по методу Фирордта веществ A и B, вычисленные в соответствие с формулами раздела 1.4. Табл. 2 Характеристики качества калибровки по методу Фирордта
Качество калибровки сильно зависит от того, какие каналы выбраны в качестве аналитических. Часто рекомендуется действовать таким образом. Строится график F(λ)= sA/sB , где sAи sB – это "чистые спектры". На нем определяют такие точки λ1 и λ2, в которых разница |F(λ1) – F(λ2)| максимальна. Способ правильный, но построить график F(λ), не зная чистых спектров, невозможно. 3.3. Непрямая калибровкаВ методе Фирордта. для калибровки используются несколько каналов – столько, сколько веществ нужно определить. Естественно обобщить этот подход, задействовав все имеющиеся у нас обучающие данные. Будем рассматривать полное уравнение классической калибровки X=СS Также как в методе Фирордта умножим его слева на транспонированную матрицу Yc
Тогда матрица –
является оценкой матрицы "чистых спектров". Заметим, что это уже не квадратная матрица – она имеет размерность A×J (В нашем примере 2×101). Сравним ее с исходной матрицей чистых спектров A и B. На Рис. 16 показаны исходные и восстановленные спектры. Различие между ними особенно заметно в той области, где велик вклад от примеси C. На краях – там, где спектр C стремится к нулю (при λ<20 и λ>60) – спектры A и B восстановлены практически идеально. К сожалению, не подозревая о существовании в системе вещества C, мы не сможем заметить этого факта.
Рис.20 Оценка матрицы "чистых спектров" в непрямой калибровке Продолжая построение
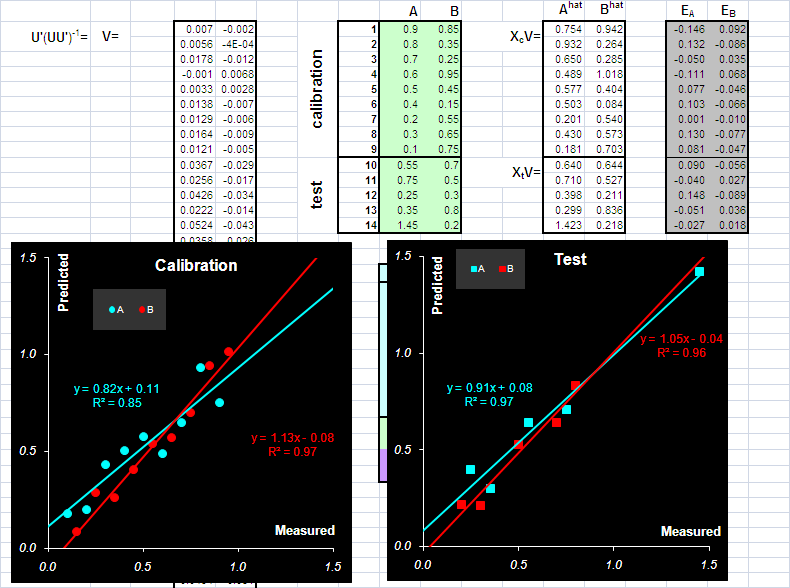
калибровки, положим в уравнении (14)
Тогда матрица размерностью (101×2) –
будет линейным "оценивателем" матрицы концентраций Y. Для того, чтобы найти оценки величин концентраций в обучающем наборе, надо матрицу V умножить на матрицу соответствующих спектров Xc –
Аналогично, для оценки концентраций в проверочном наборе, матрица V умножается на Xt –
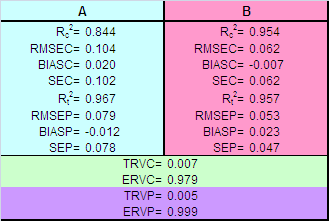
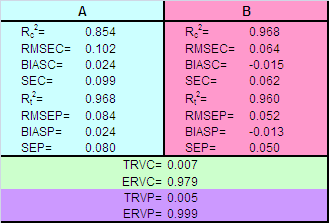
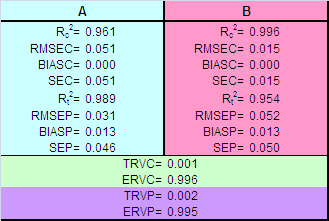
Рис.21 Оценка концентраций в непрямой калибровке В Табл. 3 приведены различные характеристики качества прямой калибровки веществ A и B, вычисленные в соответствие с формулами раздела 1.4. Табл. 3 Характеристики качества непрямой калибровки
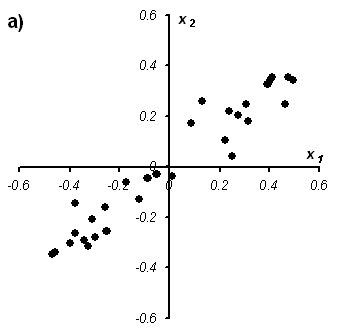
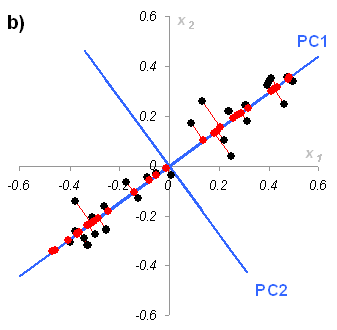
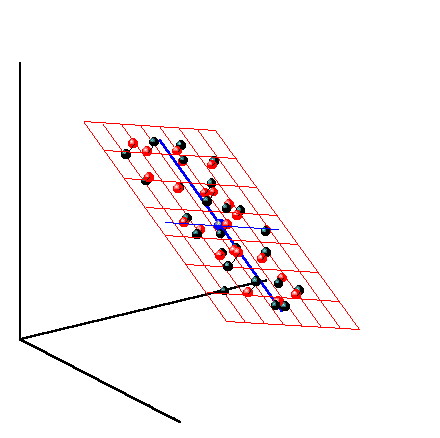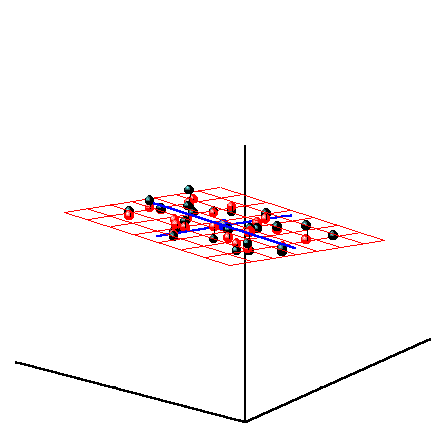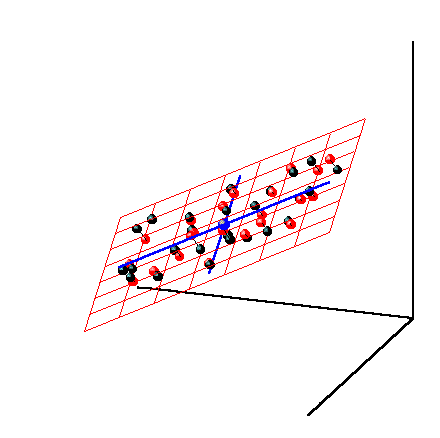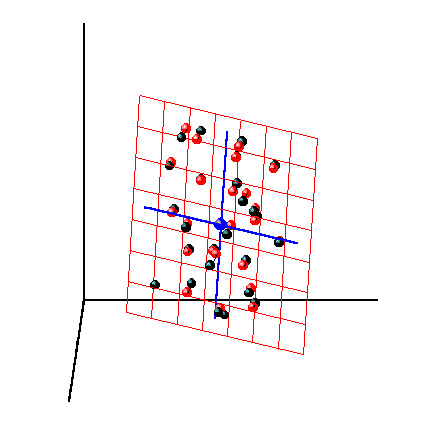
Бытует устойчивое мнение, что классическая калибровка лучше обратной. Для объяснения ее преимущества говорят, что она опирается на фундаментальные физические принципы, такие как закон Ламберта-Бэра. С точки зрения математиков, все выглядит наоборот. Во-первых, сама калибровка является "обратной" по отношению к искомым величинам Y. Во-вторых, процедура, с помощью которой оцениваются отклики, является неустойчивой. Действительно, если между искомыми концентрациями A и B имеется линейная связь, например cB ~ 0.5cA, то матрица YtY не имеет обратной, или она обращается с большой ошибкой. Линейная связь между искомыми концентрациями часто наблюдается при анализе объектов окружающей среды, в которых она обусловлена естественными причинами. В-третьих, классическая калибровка не дает нам никаких признаков отклонения системы от ее идеальной модели, например, не позволяет обнаружить примеси (вещество C). Наконец, далее мы увидим, что и качество такой калибровки (точность, прецизионность) уступает многим современным методам. 4. Обратная калибровкаВ обратной калибровке основное уравнение имеет вид (10) Y = XB в котором. искомая величина Y (концентрация) прямо выражается через известную матрицу спектров X. Хотя такое представление калибровочного уравнения и противоречит основному соотношению (14), такой подход обеспечивает лучшее качество моделирования. 4.1. Множественная калибровкаПростейшим вариантом обратной калибровки является множественная линейная регрессия (MLR). В разделе 1.7 мы уже обсуждали свойства MLR в связи с проблемой мультиколлинеарности. В частности отмечалось, что во множественной регрессии число переменных должно быть меньше числа образцов. В нашем модельном примере число калибровочных образцов равно 9, поэтому для использования MLR необходимо отобрать из 101 канала только 8 и по ним строить калибровку. Больше переменных взять нельзя, но можно меньше. На листе MLR есть активный элемент, с помощью которого можно быстро сменить первый канал; остальные изменятся автоматически.
Рис.22 Множественная линейная калибровка На Рис. 22 показано как отбираются эти каналы – равномерно, с шагом 13. Первый канал можно выбрать произвольно: от 0 до 9, тогда все последующие определяются однозначно. В результате этого отбора получается матрица независимых переменных X размерностью (14×8), состоящая из двух частей: обучающего набора (9×8) и проверочного (5×8). Используя обучающий набор переменных можно построить множественную регрессию: (10) между X и Y. Для этого можно применить формулы (11) и (12), но проще воспользоваться функцией Excel ТЕНДЕНЦИЯ.
Рис.23 Графики "измерено-предсказано" для множественной калибровки. Обучающий (a) и проверочный (b) наборы На Рис. 23 показаны графики "измерено-предсказано" для множественной калибровки. Видно, что обучающий набор "слишком хорошо" описывается моделью. А вот проверка неудовлетворительна. Здесь заметно, и смещение, и малая корреляция. В Табл. 4 приведены характеристики качества множественной калибровки веществ A и B, вычисленные в соответствие с формулами раздела 1.4. Табл. 4 Характеристики качества множественной линейной калибровки
Видно, что в этом случае мы получили типичную переоценку модели (см. раздел 1.6) – число отобранных переменных слишком велико. Попытки сменить набор переменных ситуацию не улучшают. Таким образом множественная калибровка является неприемлемым методом. Она приводит к переоценке модели и дает неудовлетворительные результаты при использовании на новом (проверочном) наборе образцов. 4.2. Пошаговая калибровкаКак мы только что видели множественная линейная калибровка неудовлетворительна – она представляет явный пример переоценки. В этом разделе мы рассмотрим пошаговую калибровку (stepwise regression, SWR), в которой отбор переменных является способом справится с переоценкой. Идея метода состоит в следующем. Пусть имеется калибровочная модель, построенная по M отобранным каналам. Добавим к ним еще один M+1-ый канал. Выбор этого дополнительного канала основан на простом принципе – добавляется тот, который дает минимум величины RMSEC. Добавление новых каналов продолжается до тех пор, пока не наступает риск переоценки, т.е. до начала роста величины RMSEP (см. раздел 1.6).
Рис.24 Пошаговая калибровка Очевидно, что наилучший результат для веществ A и B достигается для разных каналов. Поэтому "оптимальные" наборы для A и B отличаются. Для A – это каналы 24, 86, 11, 30, …, а для B – это каналы 100, 10, 95, 39,57, Именно в таком порядке каналы добавляются в соответствующие наборы. Отбор этих каналов – простая, но трудоемкая процедура, которую можно упростить, написав небольшой макрос в Excel. В пошаговой регрессии существует много способов отбора "оптимальных" переменных. Тот, который использован здесь, самый простой – выбирать тот канал, на котором достигается минимум среднеквадратичной ошибки в обучении, RMSEC.
Рис.25 Среднеквадратичные остатки обучения (RMSEC) и проверки (RMSEP) в пошаговой калибровке На Рис. 25 показано, как изменяются среднеквадратичные остатки в обучении (RMSEC) и в проверке (RMSEP) при увеличении числа каналов в SWR. В соответствие с принципом минимума RMSEP, оптимальное число каналов для вещества B – три. Это четко видно на графике. А вот выбор числа каналов для вещества A затруднителен. На соответствующем графике кривая RMSEP не имеет минимума. Так часто случается при анализе сложных данных. В рассматриваемом примере оптимальные каналы для вещества A располагаются по краям "спектральной" области – там, где влияние скрытой примеси C не существенно. Сравните Рис. 11 и Рис. 24. Поэтому SWR калибровка для вещества A никак не может "заметить" наличие вещества C. В таком сомнительном случае следует выбирать точку излома на графике RMSEP. Именно поэтому мы выбираем только два канала для вещества A.
Рис.26 Графики "измерено-предсказано" для пошаговой калибровки. Обучающий и проверочный наборы На Рис. 26 показаны графики "измерено-предсказано" для пошаговой калибровки. Здесь заметно, что описание сбалансировано уже гораздо лучше – отличие точности обучения от проверки не так существенно, как во множественной калибровке. В Табл. 5 приведены характеристики пошаговой калибровки веществ A и B, вычисленные в соответствие с формулами раздела 1.4. Табл. 5 Характеристики качества пошаговой калибровки
Подводя итог можно заметить, что пошаговая регрессия дала наилучший результат среди всех исследованных нами методов калибровки. Но есть и более точные методы. 5. Калибровка на латентных переменных5.1. Проекционные методыВ методе пошаговой калибровки использовались только два или три (наиболее информативных) канала из 101, и это позволило достичь приемлемого результата. Прочие каналы были отброшены как "излишние", не нужные. Такой подход представляется несколько расточительным – ведь отброшенные данные содержали полезную информацию, которую хорошо было бы использовать. В частности, применяя SWR, мы не заметили присутствие третьего вещества – примеси C, которая сильно проявляется как раз в этих исключенных каналах. Проблема, которую мы сейчас будет исследовать, состоит в следующем. Как использовать все имеющиеся данные (каналы), и, в то же время, избежать переоценки и мультколлинеарности, неизбежных при большом числе регрессионных переменных. Решение этой дилеммы было предложено К. Пирсоном (Karl Pearson) в 1901 году – надо использовать новые, латентные переменные ta, (a=1,…A), являющиеся линейной комбинацией исходных переменных xj (j=1,…J) – ta=pa1x1+… paJxJ или в матричном виде В этом уравнении T называется матрицей счетов (scores). Ее размерность – (I×A). Матрица P называется матрицей нагрузок (loadings). Ее размерность (A×J). E – это матрицей остатков, размерностью (I×J). Новые латентные переменные ta называются главными компонентами (Principal Components), поэтому и сам метод называется методом главных компонент (PCA). Число столбцов – ta в матрице T, и pa в матрице P – равно эффективному (химическому) рангу матрицы X. Эта величина обозначается A называется числом главных компонент (PC). Она заведомо меньше числа переменных J и числа образцов I. Для иллюстрации метода PCA, мы опять вернемся к тому, как строились модельные данные (раздел 2.4). Матрица спектров смесей X равна произведению матрицы концентраций C и матрицы спектров чистых компонентов S – формула (13). Число строк в матрице X равно числу образцов (I), и каждая ее строка соответствует спектру одного образца, снятому для J длин волн. Число строк в матрице C также равно I, а вот число столбцов соответствует числу компонентов в смеси (A=3). У матрицы чистых спектров S число строк равно числу каналов (длин волн) J, а число столбцов равно A. При анализе экспериментальных данных X, отягощенных погрешностями, представленными в формуле (13) матрицей E, эффективный ранг A может не совпадать с реальным числом компонентов в смеси. Метод главных компонент часто применяется при исследовательском анализе химических данных. В общем случае матрицы счетов T и нагрузок P уже нельзя интерпретировать как спектры и концентрации, а число главных компонент A – как число химических компонентов, присутствующих в исследуемой системе. Тем не менее, даже формальный анализ счетов и нагрузок оказывается очень полезным для понимания устройства данных. Дадим простейшую двумерную иллюстрацию метода PCA.
Рис.27
Графическая иллюстрация метода главных
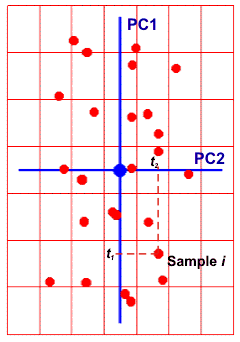
компонент. На Рис. 27 показаны данные, состоящие только из двух переменных x1 и x2, которые связаны сильной корреляцией. На соседнем рисунке те же данные представлены в новых координатах. Вектор нагрузок p1 первой главной компоненты (PC1) определяет направление новой оси, вдоль которой происходит наибольшее изменение данных. Проекции всех исходных точек на эту ось составляют вектор t1. Вторая главная компонента p2 ортогональна первой, и ее направление (PC2) соответствует наибольшему изменению в остатках, показанных отрезками, перпендикулярными оси p1. Этот тривиальный пример показывает, что метод главных компонент осуществляется последовательно, шаг за шагом. На каждом шаге исследуются остатки Ea, среди них выбирается направление наибольшего изменения, данные проецируются на эту ось, вычисляются новые остатки, и т. д. Этот алгоритм называется NIPALS. Метод главных компонент можно трактовать как проецирование данных на подпространство меньшей размерности A. Возникающие при этом остатки E рассматриваются как шум, не содержащий значимой химической информации. На Рис. 28 представлена графическая иллюстрация этого тезиса. Рис.28 Метод главных компонент – как проекция на подпространство В случае, когда метод главных компонент применяется для решения калибровочной (регрессионной) задачи он носит название регрессии на главные компоненты (Principal Component Regression, PCR). В методе PCA проекция строится только по данным X. Значения откликов Y никак не используются. Обобщением метода PCA является метод проекций на латентные структуры (Projection on Latent Structures, PLS), который сейчас является самым популярным методом многомерной калибровки. Он во многом похож на метод PCR, с тем существенным отличием, что в PLS проводится одновременная декомпозиция матриц X и Y Проекция строится согласованно – так, чтобы максимизировать корреляцию между соответствующими векторами X-счетов ta и Y-счетов ua. Поэтому PLS декомпозиция гораздо лучше описывает сложные связи, используя при этом меньшее число главных компонент.
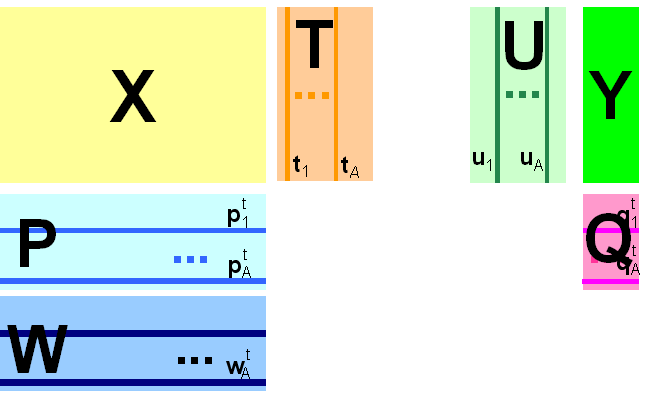
Рис. 29 Графическое представление метода проекций на латентные структуры В том случае, когда имеется несколько откликов Y (т.е. K>1), можно построить две проекции исходных данных – PLS1 и PLS2. В первом случае для каждого из откликов yk строится свое проекционное подпространство. При этом и счета T (U) и нагрузки P (W, Q) , зависят от того, какой отклик используется. Этот подход называется PLS1. Для метода PLS2 строится одно общее проекционное пространство, которое является общим для всех откликов. Следует обратить внимание на то, что и PCA, и PLS методы не учитывают свободного члена при разложении матрицы X. Это видно из формул (15) и (16). Исходно предполагается, что все столбцы матриц X и Y имеют нулевое среднее, т.е.,
Этого легко можно достичь,
проведя центрирование данных (раздел
1.8 и раздел 2.5). Но, построив
калибровочную модель на центрированных
данных, надо не забыть пересчитать
полученные оценки
Приведем некоторые полезные формулы, доказательство которых можно найти во многих учебниках по анализу многомерных данных. Во всех методах –
В методе PCR –
В методе PLS –
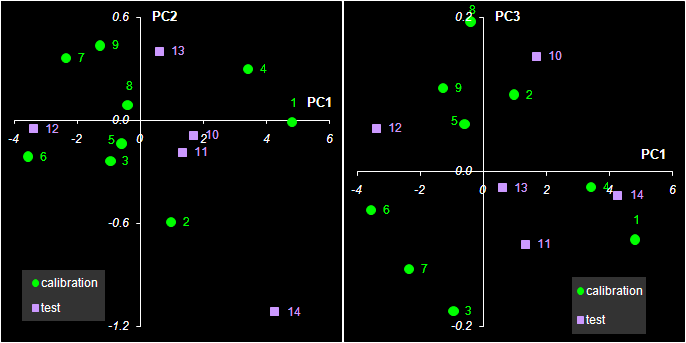
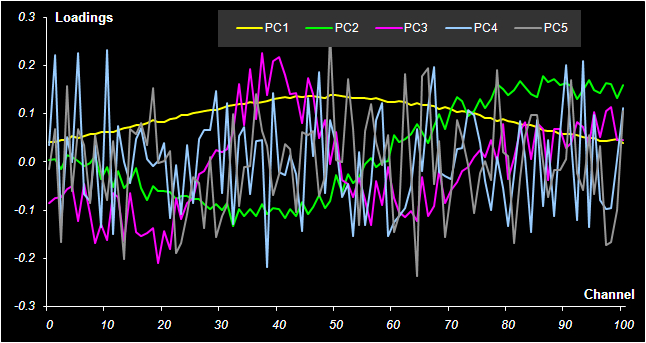
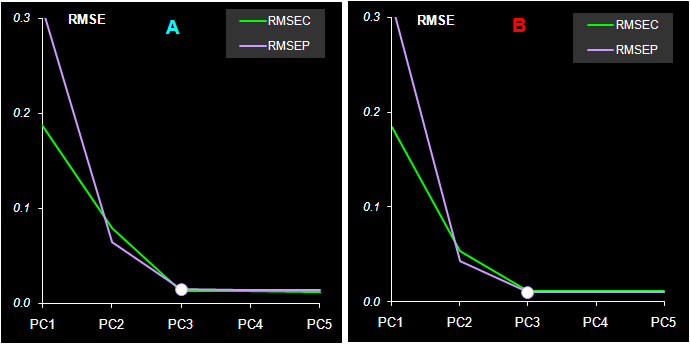
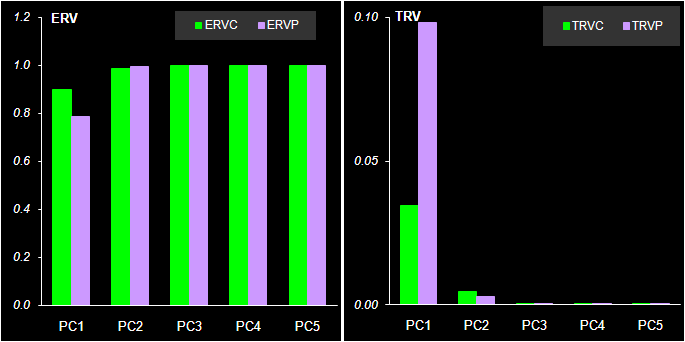
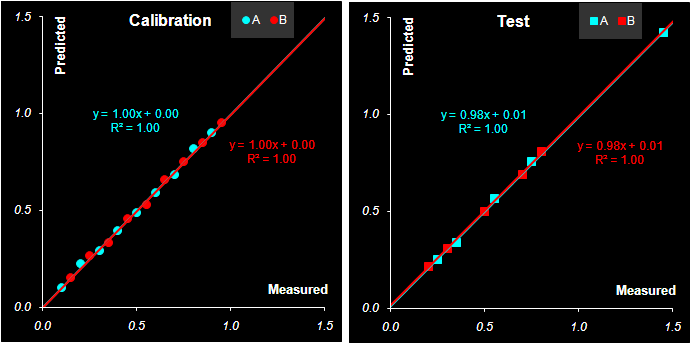
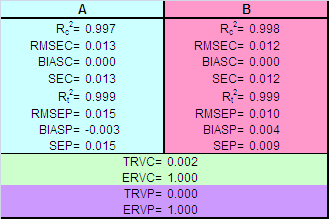
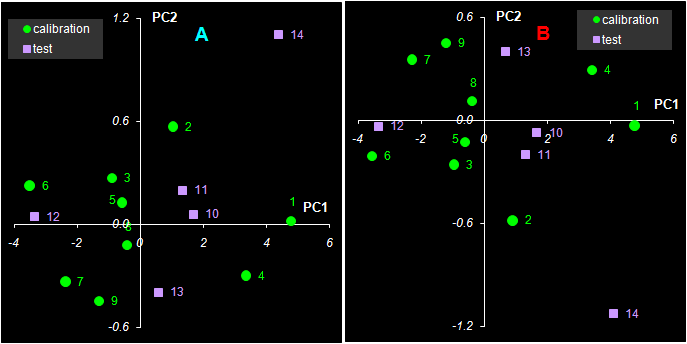
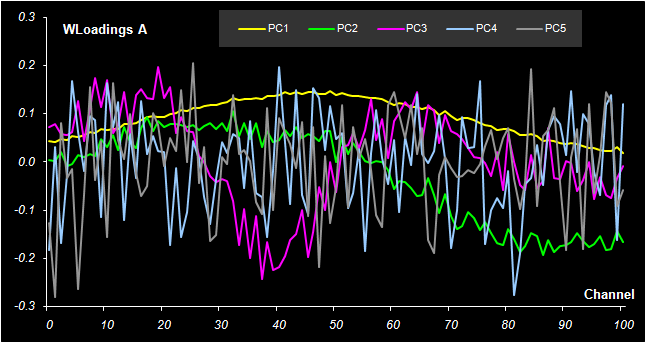
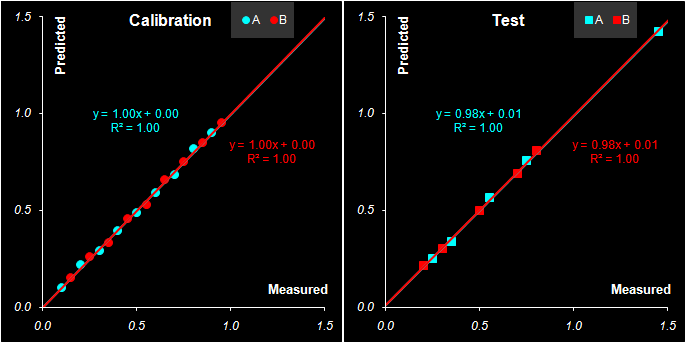
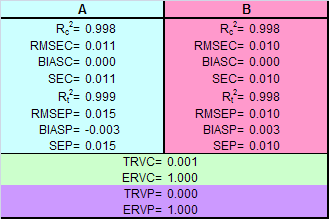
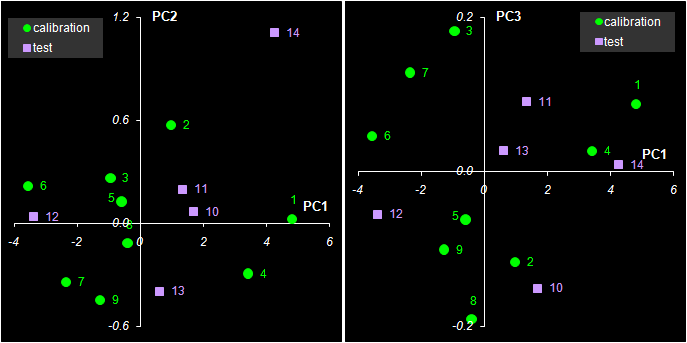
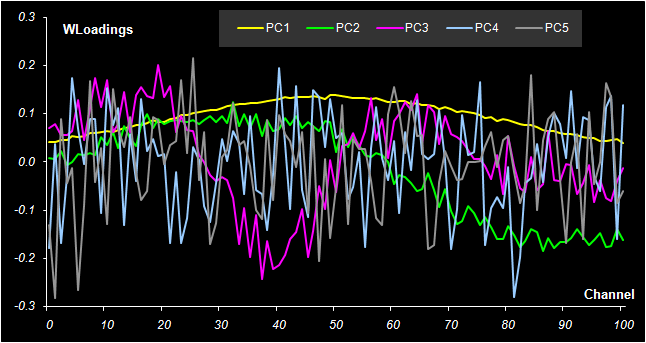
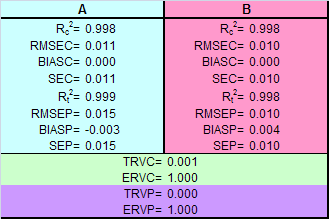
5.2. Регрессия на латентных переменныхПосле того, как данные X спроецированы на подпространство размерности A, исходная калибровочная задача (10) превращается в серию регрессий на латентных переменных T – Здесь индекс k нумерует отклики в матрице Y. Заметим, что в методах PCR и PLS2 имеется только одна матрица латентных переменных T=T1 = …= TK. Векторы bk – это неизвестные коэффициенты, а Tk – матрицы счетов. Их общая размерность A существенно меньше числа переменных J, поэтому матрица TktTk обращается устойчиво и проблема мультиколлинеарности (раздел 1.7) не существенна. Но вот другая трудность – возможность переоценки (раздел 1.6) остается, и с ней нужно уметь справляться. Для проекционных методов сложность модели целиком определяется числом главных компонент A и выбор этой величины является основной трудностью в проекционных методах. Существует много методов определения величины A – эффективной размерности многомерных данных. Выше мы уже отмечали, что часто она связана с химическим рангом системы, т.е. с числом веществ, присутствующих в системе. Однако самым универсальным способом оценки размерности A является исследование графиков величин RMSEC и RMSEP, так как это было уже сделано в разделах 1.6 и 4.2.
Рис. 30 Графики T счетов в методе PCR При построении многомерных калибровок, большое внимание уделяется графикам счетов и нагрузок. Они несут в себе информацию, полезную для понимания того, как устроены данные. На графике счетов (Рис. 30) каждый образец изображается в координатах (ti, tj), чаще всего – (t1, t2). Близость двух точек означает их схожесть. Образцы, расположенные близко к началу координат (например, образцы 5, 11), являются самыми типичными – образцовыми. Напротив, образцы, которые находятся далеко (например, образцы 1 и 14), являются подозрительными маргиналами, и, может быть, даже выбросами.
Рис. 31 Графики P нагрузок в методе PCR Если график счетов используется для анализа взаимоотношений образцов, то график нагрузок применяется для исследования роли переменных. На Рис. 31 показано как меняются нагрузки в зависимости от номера канала j. Можно обратить внимание на следующую закономерность. Чем больше номер главной компоненты, тем более зашумленным выглядит соответствующий нагрузки. График первой компоненты почти гладкий. По форме он похож на спектры чистых веществ A и B (см. Рис. 11). Вторая и третья главные компоненты отличаются более сложной формой, но они все еще имеют некоторые систематические тренды. А вот четвертая и пятые компоненты представляют просто случайный шум. Так, исследуя графики нагрузок, можно установить, что в нашем примере нужно использовать только 2 или 3 главные компоненты, но ни никак не больше трех. 5.3. Практическое применение калибровки на латентных переменныхКалибровка на латентных переменных обычно строится на центрированном обучающем наборе (Xc, Yc). Для того, чтобы получить прогноза на проверочный или новый набор образцов (Xt, Yt), их надо также сцентрировать и спроецировать на уже имеющееся подпространство. Иными словами, нужно найти счета Tt новых образцов. В методе PCR это делается очень просто – Tt=Xt P, где P – это матрица нагрузок, построенная по обучающему набору. Для методов PLS дело обстоит гораздо сложнее. Вычислительные аспекты многомерной калибровки выходят за пределы настоящего пособия. Подробное изложение всех необходимых алгоритмов, а также соответствующие MatLab коды для PCA, PLS1 и PLS2 приведены в пособии MatLab. Руководство для начинающих. Для работы с проекционными методами существуют большие коммерческие программы, например, The Unscrambler, Simca-P, которые представляют специальную среду для проведения различных манипуляций с многомерными данными. В частности, в них реализованы и все обсуждаемые методы калибровки. Среди свободно распространяемых программ можно отметить Multivariate Analysis Add-in – надстройка для Excel, разработанная в Хемометрическом центре Бристольского университета под руководством проф. Р. Бреретона. В этом пособии все проекционные вычисления (PCA/PLS) проводятся в рабочей книге Calibration.xls с помощью специальной надстройки (Add-In) к программе Excel, которое называется Chemometrics.xla. Оно дополняет список стандартных функций Excel и позволяет проводить разложение на листах рабочей книги. От том как ее установить написано в пособии Инсталляция Chemometrics Add-In, а о том как ее использовать, рассказано в пособии Проекционные методы в системе Excel. 5.4. Регрессия на главные компоненты (PCR)Рассмотрим, как применяется PCR в модельном примере. Все вычисления приведены на листе PCR. Сначала, по обучающим данным Xc, находится матрица PCA счетов Tс размерностью (9×5). Она состоит из пяти столбцов – главных компонент ta, a=1, 2, …, 5. С регрессионной точки зрения Tс – это матрица предикторов, т.е. независимых переменных. Двумя откликами будут центрированные значения концентраций веществ A и B. Затем, с помощью функции ТЕНДЕНЦИЯ (TREND) для каждого отклика строятся по пять регрессий. В этих регрессиях участвуют, соответственно, одна, две, ... , пять главных PCA компонент. Так строится PCR калибровка на обучающем наборе. В этих простых вычислениях есть одна тонкость. Регрессия строится на центрированных данных Ac и Bc только потому, что в версии Excel 2003 имеется критическая ошибка, исправленная в последующих версия, начиная с Excel 2007. Проверочные данные тоже проецируются на пространство главных компонент и для них тоже определяются PCA счета t1, …, t5. К этим счетам применяется построенная калибровка, и находятся оценки центрированных концентраций Achat. Окончательные оценки откликов Ahat для каждого числа главных компонент a получаются после учета центрирования по концентрациям Соответствующие значения среднеквадратичных остатков обучения (RMSEC) и проверки (RMSEP) показаны на Рис. 32.
Рис. 32 Среднеквадратичные остатки обучения (RMSEC) и проверки (RMSEP) в регрессии на главные компоненты Из Рис. 32 видно, что для обоих веществ минимум RMSEP достигается для трех PC (A=3). Таким образом, применив PCR, мы легко смогли установить, что в исследуемой системе присутствуют не два, а три вещества.
Рис. 33 Полная (TRV) и объясненная (ERV) дисперсии остатков в регрессии на главные компоненты На Рис. 33 показаны полная (TRV) и объясненная (ERV) дисперсии остатков. Эти графики также свидетельствуют о том, что эффективная размерность системы – три. Для трех PC объясненная дисперсия практически равна 1, а полная дисперсия близка к нулю. В тоже время, видно, что графики среднеквадратичных остатков (Рис. 32) по сравнению с графиками дисперсий (Рис. 33) более наглядны.
Рис. 34 Графики "измерено-предсказано"
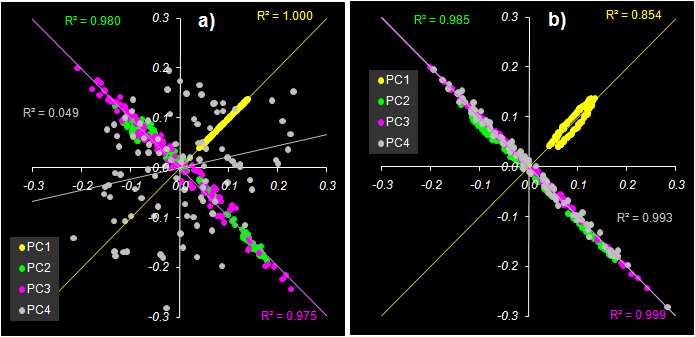
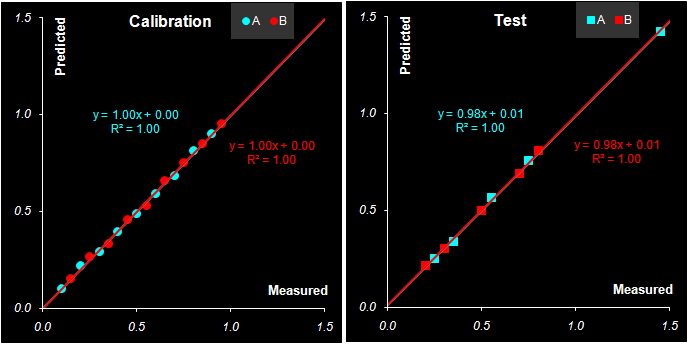
в регрессии на главные компоненты. На Рис. 34 показаны графики "измерено-предсказано" для PCR при трех главных компонентах. Результат выглядит просто идеально – высокие коэффициенты корреляции, малые сдвиги, как в обучающем, так и проверочном наборах. Сравнивая эти графики с их аналогами в других метода – Рис. 16, Рис. 19, Рис. 21, Рис. 23, Рис. 26 – можно увидеть очевидные преимущества регрессии на главные компоненты. В Табл. 6 приведены характеристики качества калибровки веществ A и B, построенной методом главных компонент. Все эти значения были вычислены в соответствие с формулами раздела 1.4. Табл. 6 Характеристики качества регрессии на главные компоненты
Таким образом, мы получили, что регрессия на главные компоненты (PCR) имеет явные преимущества в сравнении с методами классической калибровки. Этот способ моделирования точнее, имеет меньшее смещение. Это объясняется тем, что в многомерной калибровке используются все имеющиеся экспериментальные данные. При этом они модифицированы так, чтобы избежать как мультиколлинеарности, так и переоценки. 5.5. Регрессия на латентные структуры -1 (PLS1)Регрессия на латентные структуры (PLS1) очень похожа на метод PCR. Отличие состоит в том, что при построении проекционного пространства учитываются не только значения предикторов X, но и откликов Y. В результате получается не одна, а две матрицы T счетов – для каждого отклика (A и B) в отдельности.
Рис. 35 Графики T счетов в методе PLS1 На Рис. 35 показаны графики первых двух T счетов в регрессии PLS1 для откликов A и B. При кажущемся различии, они очень схожи между собой и с аналогичным графиком PC1–PC2 на Рис. 30. Чтобы это понять, достаточно изменить знаки у первой главной PLS компоненты для отклика A. Такое преобразование главных компонент вполне законно. Дело в том, что, и PCA, и PLS декомпозиции определяются неоднозначно. В эти разложения всегда можно вставить произвольную, дополнительную матрицу O, такую, что OOt=I. Действительно – X = TPt = TIPt = T (OOt) Pt = (TO) (PO)t = (Tnew) (Pnew)t.
Рис. 36. Графики весовых нагрузок W для отклика A в методе PLS1 Аналогичная картина наблюдается и для нагрузок. На Рис. 36 показаны весовые нагрузки W для отклика A. Мы используем весовые нагрузки W, а не просто нагрузки P, потому, что они, по своей сути, ближе к P нагрузкам в методе PCA. Калибровка по методу PLS1 строится вполне аналогично методу PCR, только в этом случае для каждого отклика используется своя матрица счетов.
Рис. 37 Среднеквадратичные остатки обучения (RMSEC) и проверки (RMSEP) в регрессии PLS1 На Рис. 37 показаны среднеквадратичные остатки обучения (RMSEC) и проверки (RMSEP) в регрессии PLS1. Этот график похож на свой аналог в методе PCR (Рис. 32). Здесь тоже очевидно, что минимум RMSEP достигается для трех PC (A=3). Некоторое отличие можно заметить только в поведении RMSEC – график не выходит на предел при трех PC, а продолжает падать с ростом числа компонент. В этом проявляется особенность метода проекций на латентные структуры – нацеленность на поддержание максимальной корреляции между T и U счетами.
Рис. 38 Графики "измерено-предсказано" в PLS1 регрессии. Обучающий и проверочный наборы Естественно, что и графики "измерено-предсказано" для калибровки методом PLS1 (Рис. 38) похожи на аналогичные графики для метода PCR (Рис. 34). То же можно сказать и о характеристиках качества калибровок, построенных методом PLS1, которые приведенные в Табл. 7. Табл. 7 Характеристики качества PLS1 регрессии
Таким образом, калибровка методом PLS1 для рассматриваемого модельного примера очень близка по своим свойствам к калибровке методом RCR. 5.6. Регрессия на латентные структуры -2 (PLS2)Если метод PLS1 был похож на метод PCR, то отличие между PLS1 и PLS2 в нашем примере еще менее заметно. При построении проекционного пространства PLS2 также учитываются значения и X, и Y. Однако все отклики Y рассматриваются совместно, поэтому получаются не несколько (как в PLS1), а одно общее проекционное подпространство (как в PCR) В результате мы имеем пару матриц счетов T и U, и три матрицы нагрузок P, W и Q.
Рис. 39 Графики T счетов в методе PLS2 На Рис. 39 показаны графики первых трех T счетов в регрессии PLS2. Сравнивая их с аналогичными графиками на Рис. 30 и Рис. 35, легко заметить сходство. То же самое видно и для W нагрузок, представленных на Рис. 40.
Рис. 40. Графики весовых нагрузок W в методе PLS2 Сравнивая P нагрузки в методе PCR на Рис. 31 и W нагрузки в методе PLS2, можно заметить, что между первыми тремя компонентами (нагрузками) есть хорошая линейная корреляция – для PC1 положительная (R = 0.9999), а для PC2 и PC3 отрицательная (R = –0.990, R = –0.987). Но вот четвертые компоненты уже никак не связаны друг с другом (R = 0.221). Смотри Рис. 41a). Это еще одно, дополнительное подтверждение того, что эффективная размерность исследуемой системы – три.
Рис. 41 a) Корреляция между P
нагрузками в методе PCR и W нагрузками в
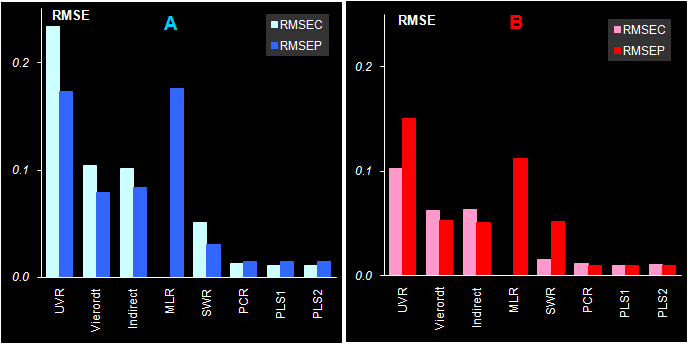
методе PLS2 Однако между методами PLS1 и PLS2 такой интересной связи не наблюдается. На Рис. 41b) показано, как связаны между собой W нагрузки, найденные методами PLS1 и PLS2. В первом случае использовались PLS1 W нагрузки для вещества B, но и для вещества A наблюдается аналогичная картина. После того, как построена проекция на PLS2 подпространство, калибровка строится также как в методе PCR.
Рис. 42 Среднеквадратичные остатки обучения (RMSEC) и проверки (RMSEP) в методе PLS2 По Рис. 42, на котором показаны среднеквадратичные остатки обучения (RMSEC) и проверки (RMSEP) в регрессии PLS2, легко определить нужное число главных компонент A=3. Отличия от аналогичного графика на Рис. 37 в методе PLS1 глазом не различимы.
Рис. 43 Графики "измерено-предсказано" в PLS2 регрессии. Обучающий и проверочный наборы Также неотличимы и графики "измерено-предсказано" для PLS1 (Рис. 38) и PLS2 (Рис. 43). Характеристики качества PLS2 калибровки, которые приведены в Табл. 8 совпадают с аналогичными для PLS1 (Табл. 7). Табл. 8 Характеристики качества PLS2 регрессии
Может сложиться впечатление, что PLS2 регрессия не дает ничего нового по сравнению с PLS1 регрессией. Действительно, в большинстве случаев так и происходит. Более того, если между откликами в матрице Y нет корреляции, то PLS1 обычно дает лучшие результаты, нежели PLS2. Для прояснения этой ситуации бывает полезно построить PCA декомпозицию для матрицы Y. Если это разложение обнаруживает связи между откликами, то метод PLS2 может оказаться очень полезным. Дальнейшее обсуждение этой интересной проблемы выходит за рамки настоящего пособия. 6. Заключение6.1. Сравнение разных методовСопоставление различных методов начнем с характеристик RMSEC и RMSEP, которые наиболее полно отражают качество моделирования.
Рис. 44 Среднеквадратичные
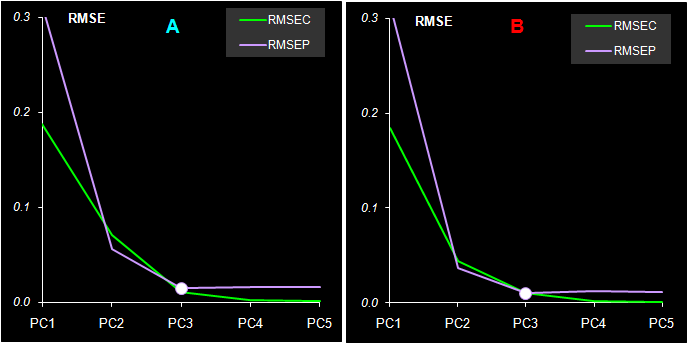
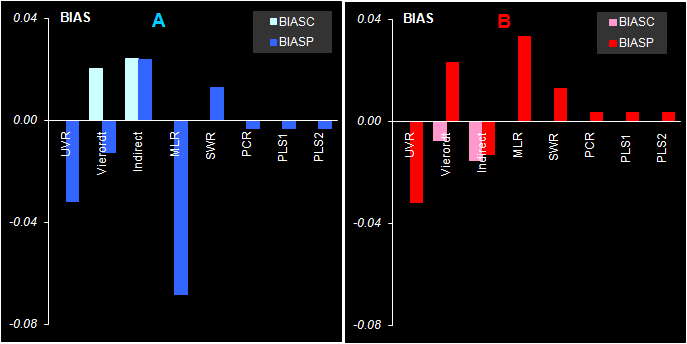
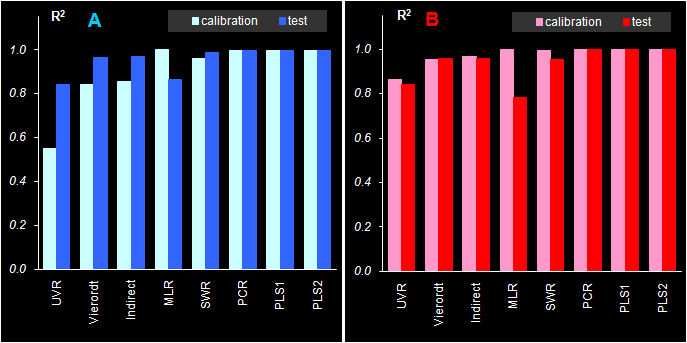
остатки обучения (RMSEC) и проверки (RMSEP) На Рис. 44 показаны среднеквадратичные остатки обучения и проверки, вычисленные для различных методов калибровки. Первое, что можно заметить на этих графиках – явное превосходство калибровки на латентных переменных: PCR, PLS и PLS2, перед традиционными подходами. Вторая интересная особенность состоит в том, что, часто, RMSEP больше, чем RMSEC. Это типично для правильной калибровки, если только различие между RMSEP и RMSEC не так разительно, как в случае множественной калибровки (MLR) или пошаговой регрессии (SWR) вещества B.
Рис. 45 Смещение в обучении (BIASC) и в проверке (BIASP) для различных методов калибровки веществ A и B На Рис. 45 представлены величины смещений, полученные на обучающей выборке (BIASC) и на проверочной (BIASP) выборке. Здесь опять мы видим превосходство проекционных методов, которые дают значительно меньшие величины систематических отклонений. Аналогично, почти всегда BIASC меньше, чем BIASP, а для UVR и MLR отличие обучения от проверки особенно заметно.
Рис. 46 Коэффициенты корреляции в обучении и в проверке для различных методов калибровки веществ A и B На Рис. 46 показаны величины коэффициентов корреляции между стандартными и оцененными откликами. Видно, что проекционные методы не только дают лучшие значения R2 (ближе к единице), но и , кроме того, представляют правильный баланс между обучением и проверкой.
Рис. 47 Стандартные ошибки в обучении (SEC) и в проверке (SEP) для различных методов калибровки веществ A и B На Рис. 47 показаны стандартные ошибки в обучении (SEC) и в проверке (SEP). Из-за того, что в нашем примере все смещения малы по сравнению с RMSE, эти графики не добавляют нам новых открытий по сравнению с уже исследованными зависимостями показанными на Рис. 44.
Рис. 48 Полная дисперсия
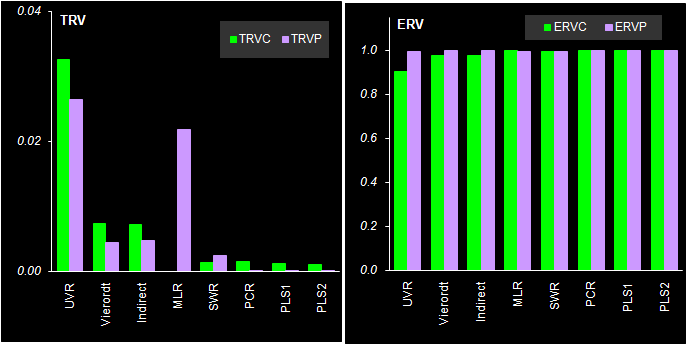
остатков в обучении (TRVC) и в проверке (TRVP) На Рис. 48 слева приведена полная дисперсия остатков в обучении (TRVC) и в проверке (TRVP), а справа – объясненная дисперсия остатков в обучении (ERVC) и в проверке (ERVP). На этих графиках мы снова видим те же закономерности, что и ранее – методы калибровки на латентных переменных лучше традиционных. Можно также отметить, что графики ERV неудобны для анализа качества моделирования – на них плохо заметны недостатки или преимущества различных методов 6.2. ВыводыПодведем итоги исследования различных методов калибровки. Итак, мы видели, что –
|
–
оценки стандартных откликов Yc,
найденные по модели, построенной на
обучающем наборе. Результатом проверки
служат величины
–
оценки проверочных откликов Yt,
вычисленные по той же модели.
Отклонение оценки от стандарта (проверочного
значения) вычисляют как матрицу
остатков: в обучении
,
и в проверке
.
откликами. Они также вычисляется
отдельно для обучающего 
и
проверочного 
наборов. 
)
и проверочные (
) данные моделями при
n=0,
1, .., 5. Видно, что при недостаточной
сложности модели (n = 0, 1) обучающие данные
лежат далеко от модели. Это – случай
недооценки. Когда сложность модели
увеличивается, то согласие между
обучающими данными и моделью
улучшается. Однако, при излишней
сложности (n = 4, 5), модель все хуже
работает при прогнозе на проверочный
набор. Это
– случай переоценки.
.
,
.
,
,
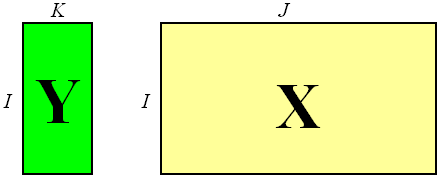
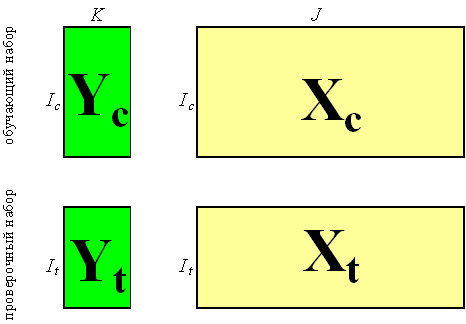
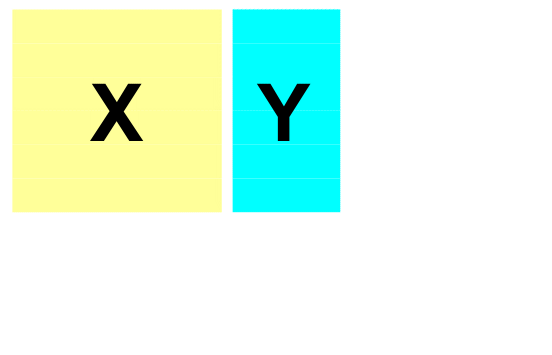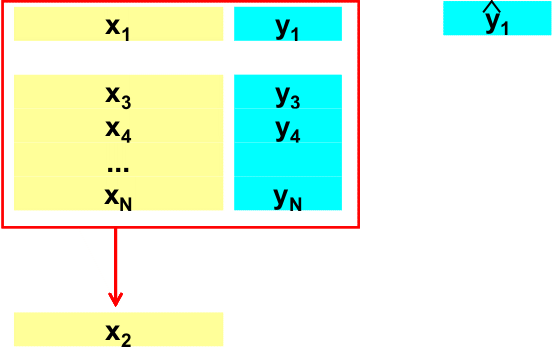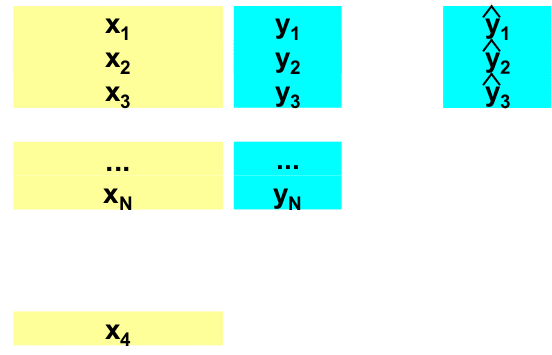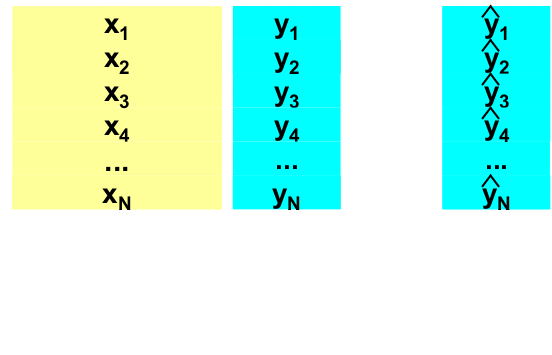
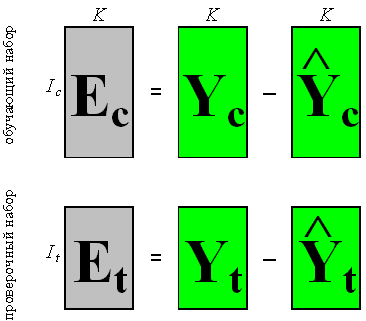
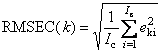
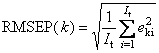
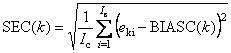
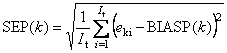
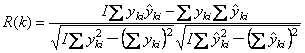
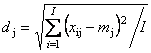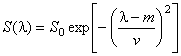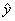найденные (предсказанные) с помощью
построенной калибровки. Такие графики
показаны на Рис. 1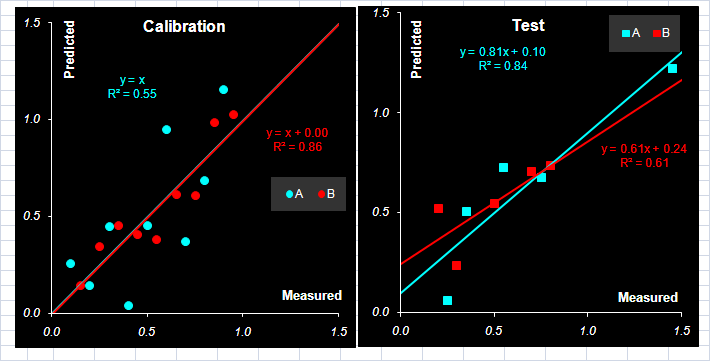
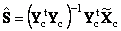
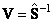
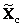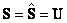имеет столько
столбцов, сколько определяется веществ (у нас 2), матрица 
и
умножим его справа на матрицу Ut
–
и
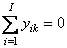для всех j=1,…, J и k=1,…, K 
,
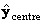добавив к ним вектор средних значений. 
