Расширение возможностей Chemometrics Add-In
- © 2010 Алексей Померанцев
Содержание
- Введение
- 1. Использование виртуальных массивов
- 1.1. Модельные данные
- 1.2. Виртуальные массивы
- 1.3. Подготовка данных
- 1.4. Декомпозиция
- 1.5. Вычисление остатков
- 1.6. Вычисление собственных значений
- 1.7. Вычисление отклонений
- 1.8. Вычисление размаха
- 2. Использование VBA программирования
- 2.1. Возможности VBA
- 2.2. Виртуализация реальных массивов
- 2.3. Подготовка данных
- 2.4. Вычисление остатков
- 2.5. Вычисление собственных значений
- 2.6. Вычисление отклонений
- 2.7. Вычисление размаха
- Заключение
Введение
В этом пособии рассказывается как вычислять некоторые важные характеристики, используемые при анализе многомерных данных. Применяя надстройку Chemometrics Add In, которая описана в пособии Проекционные методы в системе Excel, можно найти основные величины: счета и нагрузки. Но, кроме них, полезно определять и производные величины: собственные и сингулярные значения, остатки, ортогональные расстояния, и т.п.
Этот текст является естественным продолжением пособия Матричные операции в Excel, развивающим идею виртуальных массивов и VBA программирования. Поэтому рекомендуется ознакомится с материалом, изложенным в этом пособии.
Изложение иллюстрируется примерами, выполненными в рабочей книге “Tricks.xls ”, которая сопровождает этот документ.
Важная информация о работе с файлом Tricks.xls
Ссылки на примеры помещены в текст как объекты Excel. Эта книга не будут работать без использования Chemometrics Add-In.
1. Использование виртуальных массивов
1.1. Модельные данные
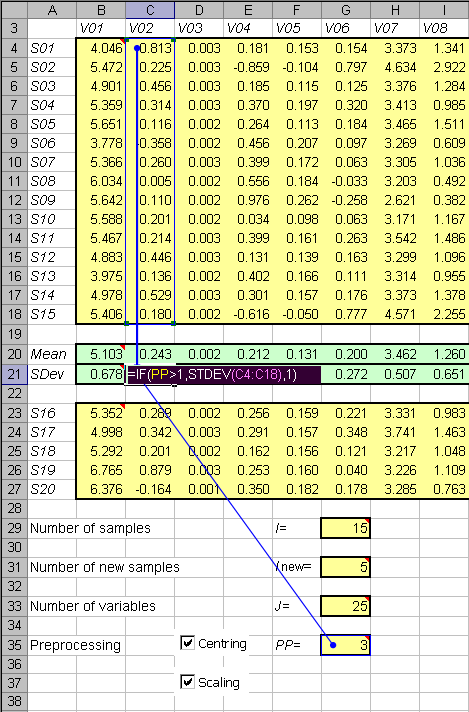
Для иллюстрации описываемых методов и приемов мы будем использовать модельные данные, которые приведены на листе Data. Они состоят из двух частей.
Первая –это обучающий (калибровочный) массив данных, который имеет имя X, определенное для всей книги. В нем содержится 15 строк (образцов) и 25 столбцов (переменных). Соответствующие значения вычисляются в ячейке G29, именованной I, – с помощью формулы ROWS(X) и, в ячейке G33, названой J,– по формуле COLUMNS(X).
Вторая часть данных – это проверочный массив, имеющий имя Xnew, определенное для всей книги. В нем содержится 5 строк (образцов). Соответствующее значение вычисляется в ячейке G31, именованной Inew, – с помощью формулы ROWS(Xnew).
Обычно, перед применением проекционных методов, данные подвергают предварительной обработке. Их центрируют и/или шкалируют. Во всех проекционных функция надстройки Chemometrics Add-In такие преобразования выполняются автоматически, за что отвечает аргумент CentWeight.
Он может принимать следующие значения
- нет ни шкалирования, ни центрирования (значение по умолчанию);
- только центрирование: вычитание среднего значения по переменной;
- только шкалирование на среднеквадратичное отклонение переменной;
- и шкалирование, и центрирование одновременно, т.е. автошкалирование.
На листе Data под этот аргумент выделена ячейка G35 с глобальным именем PP, значение в которой формируется исходя из опций, выбираемых рядом.
В принципе, для построения PCA декомпозиции нет необходимости в явном преобразовании данных на рабочем листе. Однако средние и среднеквадратичные значения могут оказаться затем полезными при вычислении различных характеристик модели. Эти величины формируются в области: B20:Z20 с именем Mean и области B21:Z21 с именем SDev. Для расчета применяются формулы, учитывающие заданное значение PP. Для средних значений используется формула
AVERAGE(С4:С18)*MOD(PP,2).
Функция MOD(PP,2) принимает значение 1 при PP=1 и 3, и 0 при PP=0 или 2.
Аналогично для среднеквадратичных отклонений используется формула
Рис.1 Модельные данные
1.2. Виртуальные массивы
При анализе данных часто возникает проблема сохранения промежуточных результатов, которые нужны не сами по себе, а только для того, чтобы вычислить по ним другие, полезные значения. Например, остатки в методе PCA часто нам не интересны, а нужны только для определения полной объясненной дисперсии, ортогональных расстояний и т.п. При этом размеры таких промежуточных массивов могут быть очень велики, да и к тому же их приходится вычислять при различных значениях числа главных компонент. Все это ведет к заполнению рабочей книги большим количеством ненужных, промежуточных результатов. Этого можно избежать, если использовать виртуальные массивы. Пример, поясняющий идею виртуального массива, приведен в пособии Матричные операции в Excel.
Рассмотрим несколько дидактических примеров, которые можно рассматривать как "образцы для подражания", полезные при решении аналогичных задач. Все они выполнены для анализа Методом Главных Компонент (PCA), но легко могут быть использованы и для задач калибровки или классификации.
1.3. Подготовка данных
Для подготовки данных в соответствие с заданными опциями, можно использовать простую формулу массива
(X–Mean)/SDev
ввод которой должен завершаться нажатием комбинации . С учетом того, как на листе Data были определены величины Mean и SDev, результат преобразования будет верен для любых комбинаций шкалирования и центрирования.
Пример преобразований обучающих – X, и проверочных – Xnew, данных приведен на листе Scaling.
1.4. Декомпозиция
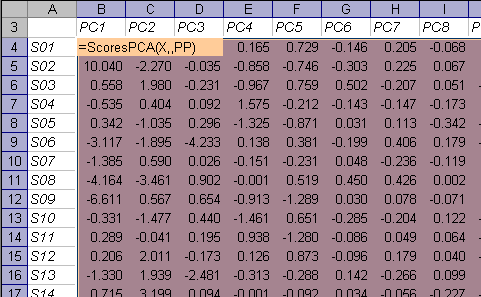
На листе Scores приведены значения PCA счетов, вычисленных с помощью функции ScoresPCA.
Рис.2 Вычисление счетов
Первый аргумент X – это имя массива данных, второй аргумент (число главных компонент) опущен, т.е. вычисляются все возможные счета. Последний аргумент – это величина PP, отвечающая за нормировку данных. Функция ScoresPCA является функцией массива, и ее ввод должен завершаться нажатием комбинации . Подробнее об этой функции можно прочитать здесь.
Матрица счетов для проверочного набора вычисляется по аналогичной формуле –
ScoresPCA(X,,PP,Xnew),
в которой однако участвует четвертый аргумент Xnew, определяющий, что счета вычисляются для нового набора данных.
Массивы, в которых выведены PCA счета имеют глобальные имена: T и Tnew соответственно.
С помощью парной функции LoadingsPCA можно найти значения нагрузок, но эти результаты мы не приводим. Дело в том, что при анализе некоторых данных (прежде всего, спектров) число переменных (длин волн) может быть очень велико (несколько тысяч). В таких случаях матрица нагрузок занимает на листе много места. Если эта матрица не нужна для каких-то особых целей, то без нее можно легко обойтись, используя виртуальные массивы.
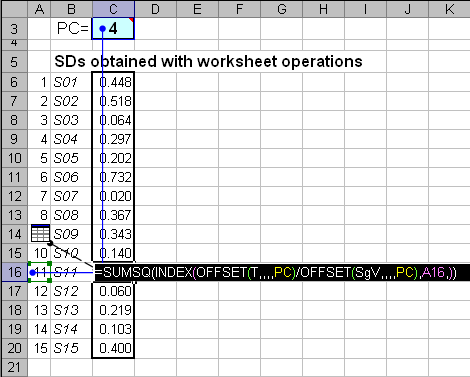
1.5. Вычисление остатков
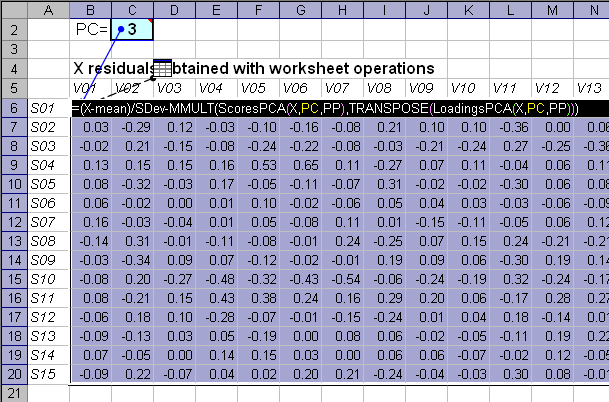
На листе Residuals показано как, с помощью виртуальных массивов, вычисляются остатки для любого значения числа главных компонент PC.Рис.3 Вычисление остатков
Для этого используется формула массива –
(X-Mean)/SDev-MMULT(ScoresPCA(X,PC,PP),TRANSPOSE(LoadingsPCA(X,PC,PP)))
Выражение –
MMULT(ScoresPCA(X,PC,PP),TRANSPOSE(LoadingsPCA(X,PC,PP)))
соответствует обычной формуле PCA –
TPt,
где T и P – это соответственно, матрицы счетов и нагрузок. Величина PC берется из ячейки C2, и, изменяя это значение, мы получаем все остатки. Выражение (X-Mean)/SDev – это матрица исходных данных, преобразованная в соответствии с заданным параметром PP.
Приведенная формула является формулой массива и ее ввод должен завершаться нажатием комбинации .
1.6. Вычисление собственных значений
На листе Eigenvalues для вычисления собственных значений и других, связанных с ними величин, используется формула массива –
SUMSQ(INDEX(ScoresPCA(X,,PP),,F3)).
Рис.4 Вычисление собственных значений
Эта формула устроена так. Сначала вычисляется виртуальный массив всех возможных счетов T = ScoresPCA(X, , PP). Затем из этого массива виртуально выделяется столбец t, соответствующий главному компоненту, номер которого указан в ячейке F4. Для этого применяется формула INDEX(T, , F4), которой отсутствует второй аргумент. Окончательный результат получается после применения функции SUMSQ(t), которая находит сумму квадратов всех элементов вектора счетов. Таким образом реализуется формула для нахождения a-го собственного значения –
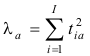 .
.
Каждое собственное значение вычисляется отдельно и оно связано с соответствующим номером PC, указанным в ячейках четвертой строки. Для этого сначала вводится одна формула для первого PC, которая затем "растаскивается" для всего набора главных компонент. Каждая формула является формулой массива и ее ввод должен завершаться нажатием комбинации CTRL+SHIFT+ENTER.
После того, как вычислены собственные значения, с их помощью можно найти и другие полезные характеристики: сингулярные значения, полную и объясненную дисперсии остатков.
Массив найденных сингулярных значений имеет глобальное имя SgV.
1.7. Вычисление отклонений
Проще всего отклонения (трансверсальные расстояния), OD –
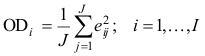
вычислять из матрицы остатков, как это показано на листе Residuals в столбце AB. Однако для этого придется выводить матрицы остатков для всех PC, что может оказаться весьма громоздко. Удобнее воспользоваться виртуальными массивами.
Рис.5 Вычисление отклонений
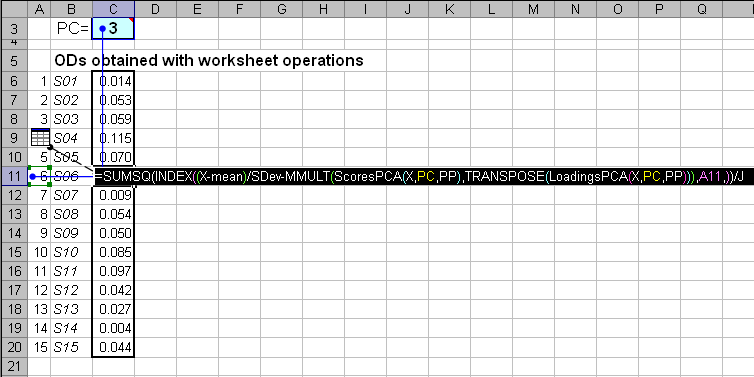
На листе OD приведена соответствующая формула. Ее внутренняя часть совпадает с приведенной в разделе 5 и дает виртуальный массив остатков E для любого значения числа главных компонент PC, заданного в ячейке C3 с именем PC –
E=(X-Mean)/SDev-MMULT(ScoresPCA(X,PC,PP),TRANSPOSE(LoadingsPCA(X,PC,PP))).
Затем из этого массива вырезается виртуальная строка ei с номером i, заданным в ячейке A11 –
ei= INDEX(E,A11,).
Отметим отсутствие последнего аргумента в функции INDEX.
Окончательный результат получается после применения функции
ODi=SUMSQ(ei)/J,
которая находит сумму квадратов всех остатков для образца i.
Величины трансверсальных расстояний для проверочного массива Xnew вычисляются по аналогичной формуле –
SUMSQ(INDEX((Xnew-Mean)/SDev-MMULT(ScoresPCA(X,PC,PP,Xnew),TRANSPOSE(LoadingsPCA(X,PC,PP))),A23,))/J,
в которой, однако, дважды участвует имя проверочного массива Xnew – в нормировке, и при вычислении счетов.
Каждая величина ODi вычисляется отдельно. Она связана с соответствующим номером образца, указанным в ячейках столбца A. Для этого сначала вводится одна формула для первого образца, которая затем "растаскивается" для всех остальных образцов. Каждая формула является формулой массива и ее ввод должен завершаться нажатием комбинации
1.8. Вычисление размаха
Для вычисления размаха (или расстояния Махаланобиса в пространстве счетов), SD –
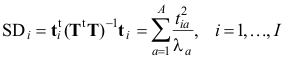
можно также воспользоваться техникой виртуальных массивов. Но сначала нужно будет найти матрицу счетов, и строку сингулярных значений. Счета были вычислены на листе Scores (глобальные имена T и Tnew), а массив сингулярных значений – на листе Eigenvalues (глобальное имя SgV)
Рис.6 Вычисление размаха
Для вычисления SDi применяется формула –
SUMSQ(INDEX(OFFSET(T,,,,PC)/OFFSET(SgV,,,,PC),A11,)).
Внутренние функции OFFSET(T,,,,PC) и OFFSET(SgV,,,,PC) вырезают из массивов T и SgV ровно PC первых столбцов. Величина PC определяется в ячейке C3 с именем PC. После деления виртуальной матрицы урезанных счетов на строку урезанных сингулярных значений, получается виртуальный массив нормированных счетов U. После этого функция INDEX(U,A11,) выбирает из массива U одну строку ui, номер которой определен в ячейке A11. Окончательный результат получается после применения функции
SDi=SUMSQ(ui),
которая находит сумму квадратов для образца i.
Для проверочного массива формула аналогична –SUMSQ(INDEX(OFFSET(Tnew,,,,PC)/OFFSET(SgV,,,,PC),A23,)).
Каждая величина SDi вычисляется отдельно. Она связана с соответствующим номером образца, указанным в ячейках столбца A. Для этого сначала вводится одна формула для первого образца, которая затем "растаскивается" для всех остальных образцов. В рассматриваемой формуле нельзя заменить матрицу T на формулу ScoresPCA(X,,PP), потому что в функции OFFSET первый аргумент не может быть виртуальным массивом.
Каждая формула является формулой
массива и ее ввод
должен завершаться нажатием комбинации
CTRL+SHIFT+ENTER
2. Использование VBA программирования
2.1. Возможности VBA
Альтернативным способом расширения надстройки Chemometrics Add In является VBA программирование, т.е. создание собственных функций листа для решения тех или иных задач. В пособии Матричные операции в Excel мы вкратце описали принципы такого программирования. Сейчас мы покажем на примерах, как использовать функции надстройки Chemometrics при написании VBA программ.
Мы ограничимся только несколькими примерами, демонстрирующими альтернативные решения тех же задач PCA анализа, что были рассмотрены в первой части этого пособия. Мы намерено не расширяем список полезных функций, оставляя читателю возможность проделать полезные упражнения и создать свою собственную библиотеку функций листа, расширяющих возможности стандартной надстройки Chemometrics Add In.
При написании новых пользовательских функций, использующих функции из надстройки Chemometrics, не забывайте установить ссылку на эту надстройку. Для этого в меню редактора Visual Basic надо выбрать и затем поставить галочку напротив Chemometrics. После этого в окне появится раздел со ссылкой внутри (см. Рис 9)
2.2. Виртуализация реальных массивов
Первая задача, которую мы рассмотрим является подготовительной процедурой, необходимой практически во всех программных модулях.
На листах рабочей книги находятся реальные массивы данных, которые мы хотим использовать в VBA программах. Для этого их нужно виртуализовать, т.е. создать в памяти компьютера виртуальный массив, содержащий те же значения, что и его реальный прототип.
Эту задачу решает функция
ConvertRange код которой приведен на Рис. 7.
Private Function ConvertRange(X As Variant) As Variant |
Рис.7 Функция ConvertRange
Код функции ConvertRange приведен в книге Tricks.xls , в модуле Utils.
2.3. Подготовка данных
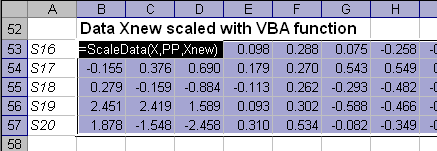
Для автоматической подготовки данных можно использовать функцию ScaleData, которая возвращает преобразованные данные по заданным значениям матриц X и Xnew.
Синтаксис
ScaleData (X [,CentWeightX] [, Xnew])
X – множество значений X (калибровочный набор)
CentWeightX – необязательный аргумент. Целая величина, определяющая проводится ли центрирование и/или шкалирование X переменных.
Xnew – необязательный аргумент. Множество новых значений Xnew (проверочный набор) для которых вычисляются и выводятся преобразованные данные.
Примечания
-
Матрица новых значений Xnew должна иметь столько же столбцов (переменных), как и матрица X.
-
Если аргумент Xnew опущен, то предполагается, что он совпадает с массивом X.
-
Результат является массивом (матрицей), той же размерности, что и Xnew.
Пример
Пример использования функции ScaleData приведен на листе Scaling.
Рис. 8 Пример использования функции ScaleData
Код функции ScaleData приведен в книге Tricks.xls, в модуле Utils.
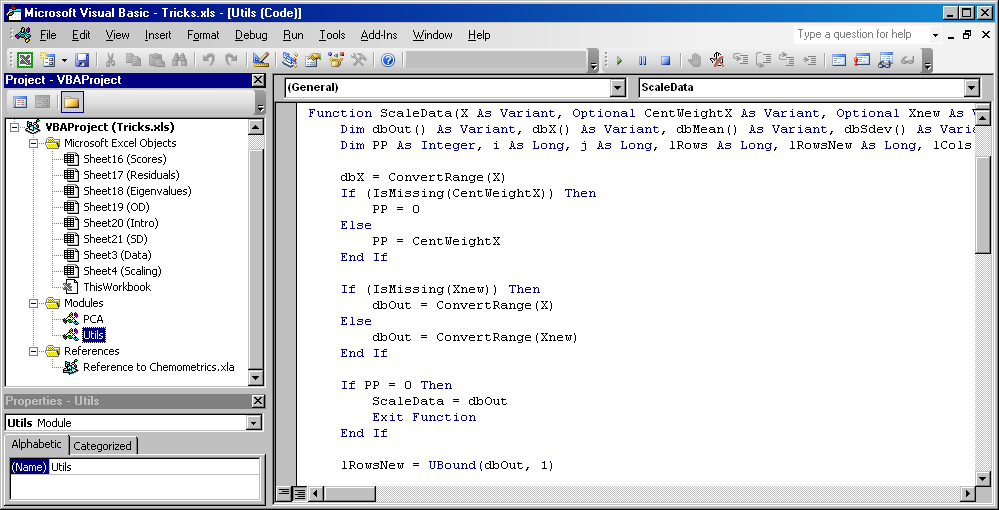
Рис.9 Код функции ScaleData
Функция ScaleData является формулой массива и ее ввод должен завершаться нажатием комбинации CTRL+SHIFT+ENTER.2.4. Вычисление остатков
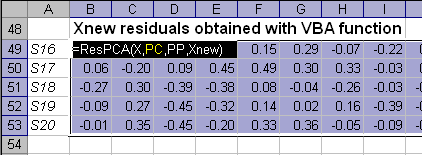
Для вычисления остатков можно использовать функцию ResPCA, которая возвращает матрицу остатков по заданным матрицам X и Xnew.
Синтаксис
ResPCA ((X [, PC] [,CentWeightX] [, Xnew])
X – множество значений X (калибровочный набор)
PC – необязательный аргумент. Целая величина, определяющая число главных компонент (A), используемых в PCA.
CentWeightX – необязательный аргумент. Целая величина, определяющая проводится ли центрирование и/или шкалирование X переменных.
Xnew – необязательный аргумент. Множество новых значений Xnew (проверочный набор) для которых вычисляются и выводятся значения остатков.
Примечания
-
Матрица новых значений Xnew должна иметь столько же столбцов (переменных), как и матрица X.
-
Если аргумент Xnew опущен, то предполагается, что он совпадает с массивом X.
-
Результат является массивом (матрицей), той же размерности, что и Xnew.
-
Аналогичная функция Chemometrics Add in: ScoresPCA
Пример
Пример применения функции ResPCA показан листе Residuals.
Рис. 10 Пример использования функции ResPCA
Функция ResPCA является формулой массива и ее ввод должен завершаться нажатием комбинации CTRL+SHIFT+ENTER.
Код функции ResPCA приведен в книге Tricks.xls в модуле PCA.
2.5. Вычисление собственных значений
Для вычисления собственных значений можно использовать функцию EigenPCA, которая возвращает одно собственное значение с номером PC по заданной матрице X.
Синтаксис
EigenPCA ((X , PC [,CentWeightX])
X – множество значений X (калибровочный набор)
PC – целое число, определяющие главную PCA компоненту, для которой вычисляется собственное значение.
CentWeightX – необязательный аргумент. Целая величина, определяющая проводится ли центрирование и/или шкалирование X переменных.
Примечания
-
Результат является числом
Пример
На листе Eigenvalues представлен пример использования функции EigenPCA для вычисления собственных значений.
Рис. 11 Пример использования функции EigenPCA
Функция EigenPCA не является формулой массива и ее ввод может завершаться нажатием клавиши ENTER.
Код функции EigenPCA приведен в книге Tricks.xls , в модуле PCA.
2.6. Вычисление отклонений
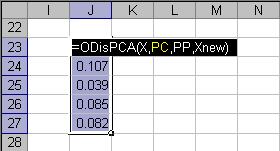
Для вычисления отклонения (трансверсальных расстояний) можно использовать функцию ODisPCA , которая возвращает столбец расстояний для заданного числа ГК, по заданным матрицам X и Xnew.
Синтаксис
ODisPCA ((X [, PC] [,CentWeightX] [, Xnew])
X – множество значений X (калибровочный набор)
PC – необязательный аргумент. Целая величина, определяющая число главных компонент (A), используемых в PCA.
CentWeightX – необязательный аргумент. Целая величина, определяющая проводится ли центрирование и/или шкалирование X переменных.
Xnew – необязательный аргумент. Множество новых значений Xnew (проверочный набор) для которых вычисляются и выводятся значения отклонений.
Примечания
-
Матрица новых значений Xnew должна иметь столько же столбцов (переменных), как и матрица X.
-
Если аргумент Xnew опущен, то предполагается, что он совпадает с массивом X.
-
Результат является массивом (матрицей), той же размерности, что и Xnew.
-
Аналогичная функция Chemometrics Add in: ScoresPCA
Пример
Пример использования функции ODisPCA приведен на листе OD.
Рис. 12 Пример использования функции ODisPCA
Функция ODisPCA является формулой массива и ее ввод должен завершаться нажатием комбинации CTRL+SHIFT+ENTER.
Код функции ODisPCA приведен в книге Tricks.xls , в модуле PCA.
2.7. Вычисление размаха
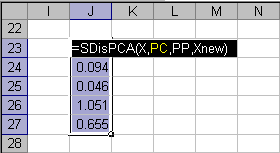
Для вычисления размаха можно использовать функцию SDisPCA, которая возвращает столбец этих величин для заданного числа ГК, по заданным матрицам X и Xnew.
Синтаксис
SDisPCA ((X [, PC] [,CentWeightX] [, Xnew])
X – множество значений X (калибровочный набор)
PC – необязательный аргумент. Целая величина, определяющая число главных компонент (A), используемых в PCA.
CentWeightX – необязательный аргумент. Целая величина, определяющая проводится ли центрирование и/или шкалирование X переменных.
Xnew – необязательный аргумент. Множество новых значений Xnew (проверочный набор) для которых вычисляются и выводятся значения расстояний.
Примечания
-
Матрица новых значений Xnew должна иметь столько же столбцов (переменных), как и матрица X.
-
Если аргумент Xnew опущен, то предполагается, что он совпадает с массивом X.
-
Результат является массивом (матрицей), той же размерности, что и Xnew.
-
Аналогичная функция Chemometrics Add in: ScoresPCA
Пример
Пример использования функции SDisPCA приведен на листе SD.
Рис. 13 Пример использования функции SDisPCA
Функция SDisPCA является формулой массива и ее ввод должен завершаться нажатием комбинации CTRL+SHIFT+ENTER.
Код функции SDisPCA приведен в книге Tricks.xls , в модуле PCA.
Заключение
Рассмотренные приемы работы с виртуальными массивами в надстройке Chemometrics могут показаться слишком сложными. Однако приведенные формулы следует рассматривать прежде всего как шаблоны для использования в своей рабочей книге. Их можно просто копировать (как текст) и вставлять в нужное место. Небольшое последующее редактирование (уточнение имен ячеек и массивов) приведет эту формулу к нужному виду.
Примеры VBA программирования призваны помочь пользователю облегчить работу с надстройкой Chemometrics. Используйте их как образцы для написания своих собственных пользовательских функций. После того, как таких функций накопится достаточно много и они будут проверены на практике, их можно собрать в отдельную книгу и превратить в новую надстройку Chemometrics Plus.